I need help in doing this homework, I'm not quite sure where to start coding... everything is provided in the pics below

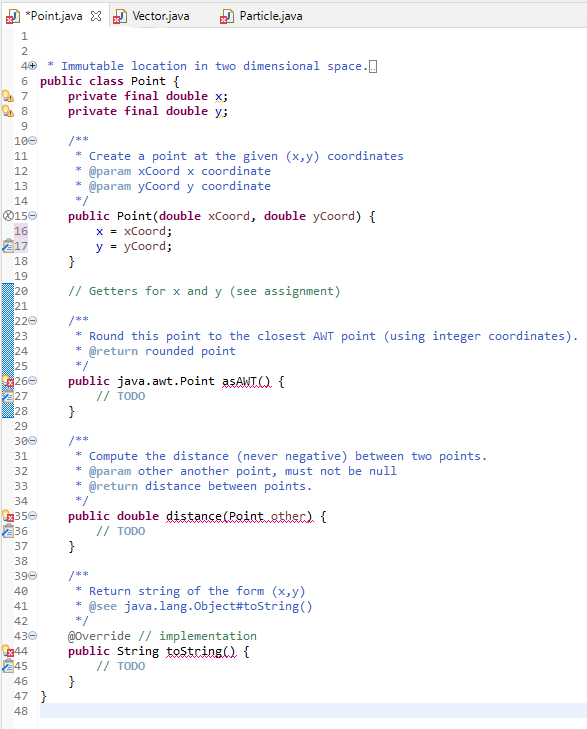
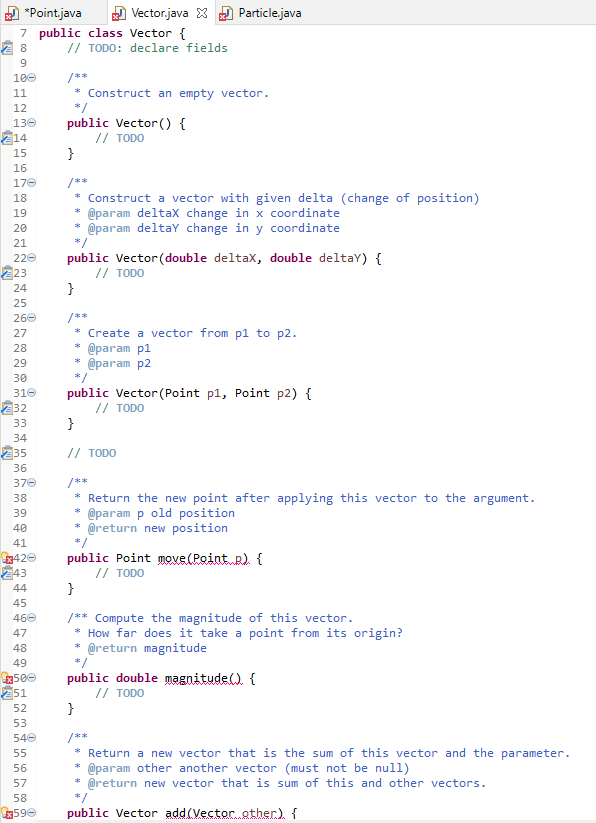
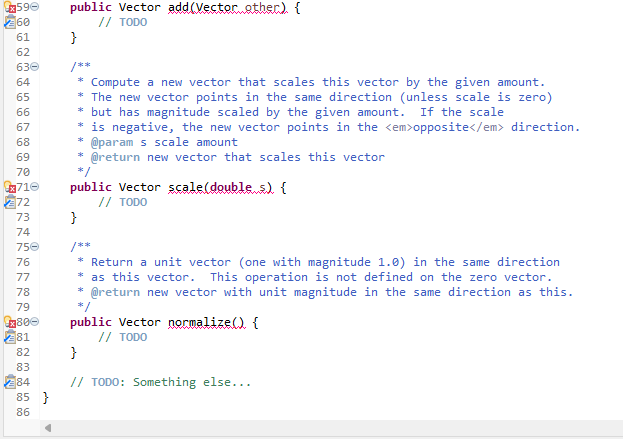
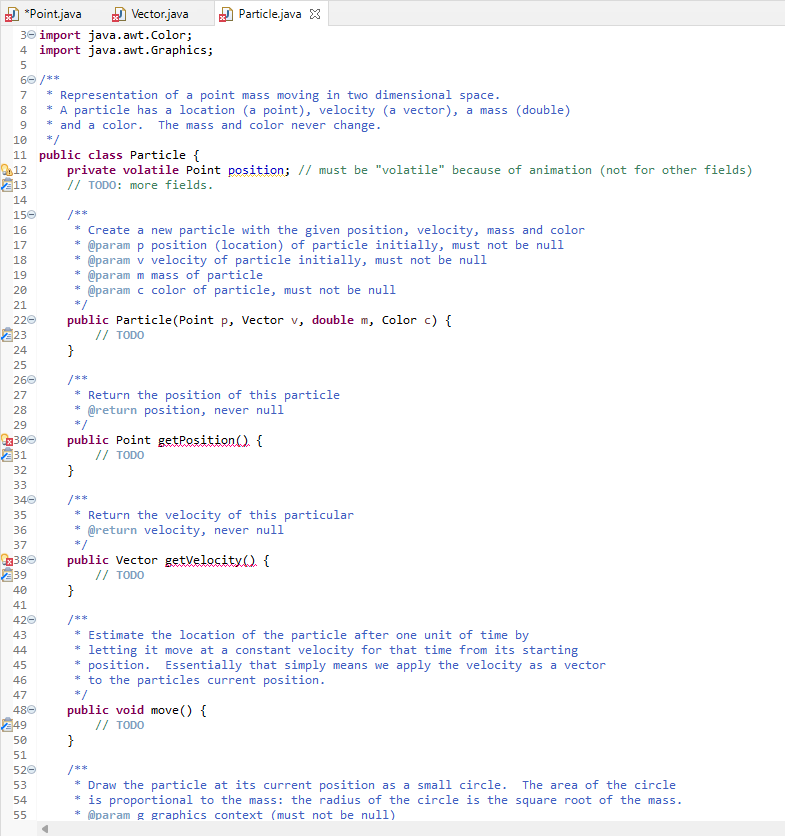
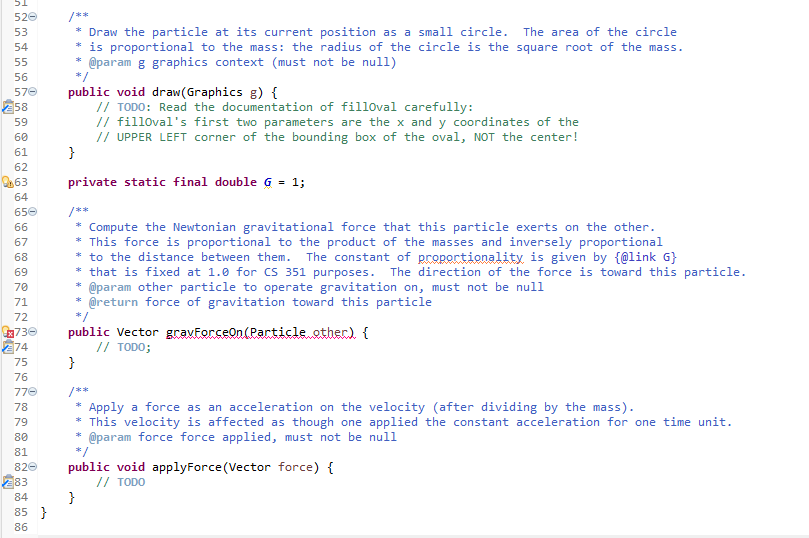
1 Concerning the ADT Point A Point is a simple immutable class with two fields of type double. By immutable," we mean that the fields are declared final. Since the fields cannot be modified after construction, the instances of the class are essentially frozen ("immutable"). Immutable objects are easy to reason about, since they don't change their values. Elsewhere, we will deal with mutable objects and then we need to worry about "aliases," with which a mutation performed in one context will cause (surprising) changes observable in a different context. The Point class provides the following operations: Point (double,double) The constructor. x() Returns the first field. (Traditionally, this method would be named getX().) y() Returns the second field. toString Returns a string of the form (x,y), for example "(3.0,-1.5)". Always have at least one digit before and after the decimal point. asAWT Return an AWT point with integer coordinates which round the double fields. distance(Point) Returns the distance to the other point from here. This is done by computing the magnitude of the vector between them (see next class). 2 Concerning the ADT Vector A Vector represents a direction (in two dimensional space). We use it to represent velocities (directed movement) of particles. A Vector is implemented as an immutable class with two double fields (dx and dy) and the following operations: Vector() Create the empty vector (no movement). Vector(double double) Create the vector with the given amounts. Vector(Point, Point) Create the vector from the first point to the second. If the first point is (1, 2) and the second point is (3,0), then the resulting vector should be (2,-2). dx() Returns movement in "x" direction. Do not confuse our Vector ADT with the deprecated Java library class java.util. Vector. They are completely different. dy() Returns movement in "y" direction. toString() Return the same sort of string as for class Point, except with angle brackets, e.g. "". move(Point) Apply this vector to the point returning a new point. If this vector is (2,-2) and the argument point is (1, 2), then the resulting point should be (3,0). add(vector) Return the new vector which combines the direction of this vector with the parameter vector. Adding (2, -2) and (1,1) is (3,-1). scale(double) Return the new vector scaled by the parameter; scaling the vector v by r is written cv. If you scale by 2, the new vector will go twice as far in both "x" and "y" directions. If you scale by -1, you get a vector in the equal but opposite direction. If (2,-2) is scaled by -0.5, the result is (-1,1). magnitude() Return the magnitude of the vector-how big a change it represents. Written |v, the magnitude of a vector can be computed using the formula |, y) = x2 + y2. For example, the magnitude of (-3, 4) is 5. normalize() A convenience method that returns a new vector which has the same direction but magnitude 1. It is computed by scaling the vector with the inverse of the magnitude: ' v For example, the normalization of (-3,4) is the unit vector (-0.6,0.8). Normalization is undefined for the zero vector (that is, you don't need to handle that case). 3 Concerning the ADT Particle a A Particle is a mutable class with four fields: position a Point; velocity a Vector; mass a double indicating how "big" the particle is; color a color for rendering purposes. The mass and color of a particle do not change and should be declared as final.) It provides the following operations: Particle(Point, Vector,double,Color) Initialize a particle. None of the arguments may be null. get Position The obvious getter. get Velocity Another obvious getter. move Advance the position by the velocity, using the move operation of Vector. = m apply Force(Vector force) Using Newton's law F = ma rewritten as a = F (using scale on the force F), update the velocity v = v+ta (using add()), where t = 1. gravForceOn(Particle) Return the gravitational force (as a Vector) that this particle exerts on the other particle. Do not modify either this or the other particle! The result is the scaled unit vector (Guzma) 421 where G is the gravitational constant (for this simulation, use G = 1), mi are the masses of the two particles, d is the distance between the two particles and u21 is the normalization of V21, the vector from the second (other) particle's position to that of the first (this). This method can assume that the argument particle is not null and that it is at a different location. (If the two particles coincided, then d = 0 would cause the computation to blow up.) Your code should use methods of the Vector and Point ADTs to do most of the work. We will penalize code that calls the x() or dx() methods directl draw(Graphics g) Draw the particle as a a disk (filled oval) with radius equal to the square root of the mass at its AWT position in the graphics context. We don't need a getMass method, since a method of the same class can access private fields. 4 Driver Program As well as an JUnit test suite for each ADT (and each with some tests locked"), we provide a program to test your ADTs with, a gravity simulation reached through a class Main. The picture starts with the following and then the "planets" move around the "sun." The orbits are not stable, and soon the system decays into chaos. Feel free to alter Main.java to try other possibilities. Particle Simulation | *Point.java X J Vector.java 1 Particle.java 2 4+ 12 14 217 * Immutable location in two dimensional space.. 6 public class Point { 7 private final double x; 8 private final double y; 9 100 /** 11 * Create a point at the given (x,y) coordinates * @param xCoord x coordinate 13 @param yCoord y coordinate */ $150 public Point(double xCoord, double yCoord) { 16 x = xCoord; y = yCoord; 18 } 19 20 // Getters for x and y (see assignment) 21 220 /** 23 * Round this point to the closest AWT point (using integer coordinates). 24 @return rounded point 25 */ x266 public java.awt.Point asAwt.Q. { 27 // TODO 28 } 29 300 /** 31 Compute the distance (never negative) between two points. 32 * @param other another point, must not be null 33 @return distance between points. 34 */ 42350 public double distance (Point other) { 236 // TODO 37 } 38 390 /** 40 * Return string of the form (x,y) 41 @see java.lang.Object#toString() 42 */ 430 @Override // implementation 244 public String toString({ // TODO 46 } 47 } 48 245 *Point.java Vector.java X Particle.java 7 public class Vector { 28 // TODO: declare fields 9 100 /** 11 * Construct an empty vector. 12 */ 136 public Vector() { 214 // TODO 15 } 16 176 /** 18 Construct a vector with given delta (change of position) 19 @param deltax change in x coordinate 20 @param deltay change in y coordinate 21 220 public Vector (double deltax, double deltay) { 223 // TODO 24 } 25 266 /** 27 * Create a vector from pl to p2. 28 @param p1 29 @param p2 30 */ 310 public Vector (Point pl, Point p2) { 232 // TODO 33 } 34 235 // TODO 36 37 /** 38 * Return the new point after applying this vector to the argument. 39 * @param p old position 40 * @return new position 41 */ 6342 public Point move(Point) { 243 // TODO 44 } 45 460 /** Compute the magnitude of this vector. 47 * How far does it take a point from its origin? 48 @return magnitude 49 13500 public double magnitude() { 251 // TODO 52 } 53 540 /** 55 Return a new vector that is the sum of this vector and the parameter. 56 @param other another vector (must not be null) 57 @return new vector that is sum of this and other vectors. 58 */ 2590 public Vector add (Vector.other). { F * public Vector add(vectorather) { // TODO } x 596 260 61 62 630 64 65 66 67 68 69 /** Compute a new vector that scales this vector by the given amount. * The new vector points in the same direction (unless scale is zero) * but has magnitude scaled by the given amount. If the scale * is negative, the new vector points in the opposite direction. * @param s scale amount * @return new vector that scales this vector */ public Vector scale(doublems) { // TODO } 70 Ex716 272 73 74 750 76 77 78 79 4800 281 82 83 * Return a unit vector (one with magnitude 1.0) in the same direction as this vector. This operation is not defined on the zero vector. * @return new vector with unit magnitude in the same direction as this. public Vector normalize() { // TODO } 84 85} // TODO: Something else... 86 8 9 150 16 17 18 19 223 *Point.java Vector.java Particle.java X 3e import java.awt.Color; 4 import java.awt.Graphics; 5 60 /** 7 * Representation of a point mass moving in two dimensional space. * A particle has a location (a point), velocity (a vector), a mass (double) * and a color. The mass and color never change. 10 */ 11 public class Particle { 9.12 private volatile Point position; // must be "volatile" because of animation (not for other fields) 213 // TODO: more fields. 14 /** * Create a new particle with the given position, velocity, mass and color @param p position location) of particle initially, must not be null @param v velocity of particle initially, must not be null @param m mass of particle 20 @param c color of particle, must not be null 21 */ 220 public Particle(Point p, Vector v, double m, Color c) { // TODO 24 } 25 260 /** 27 Return the position of this particle 28 * @return position, never null 29 */ 43300 public Point getPosition() { 231 // TODO 32 } 33 340 /** 35 * Return the velocity of this particular 36 @return velocity, never null 37 */ 2380 public Vector getvelocity. { 239 // TODO 40 } 41 420 43 * Estimate the location of the particle after one unit of time by 44 * letting it move at a constant velocity for that time from its starting 45 position. Essentially that simply means we apply the velocity as a vector 46 * to the particles current position. 47 */ 480 public void move() { 249 // TODO 50 } 51 520 /** 53 Draw the particle at its current position as a small circle. The area of the circle 54 * is proportional to the mass: the radius of the circle is the square root of the mass. 55 @param g graphics context (must not be null) M /** * 31 520 53 /** * Draw the particle at its current position as a small circle. The area of the circle * is proportional to the mass: the radius of the circle is the square root of the mass. @param & graphics context (must not be null) public void draw(Graphics ) { // TODO: Read the documentation of filloval carefully: 11 filloval's first two parameters are the x and y coordinates of the // UPPER LEFT corner of the bounding box of the oval, NOT the center! } private static final double G = 1; /** 54 55 56 570 258 59 60 61 62 24.63 64 650 66 67 68 69 70 71 72 4x730 274 75 76 770 78 79 80 81 820 83 84 * Compute the Newtonian gravitational force that this particle exerts on the other. * This force is proportional to the product of the masses and inversely proportional * to the distance between them. The constant of proportionality is given by {@link G} * that is fixed at 1.0 for CS 351 purposes. The direction of the force is toward this particle. @param other particle to operate gravitation on, must not be null * @return force of gravitation toward this particle public vector gravferseon(Particle.ether) { // TODO; } /** Apply a force as an acceleration on the velocity (after dividing by the mass). This velocity is affected as though one applied the constant acceleration for one time unit. @param force force applied, must not be null public void applyForce (Vector force) { // TODO } * 85} 86