Section 6.1 Reading Assignment: Volumes using Cross Sections

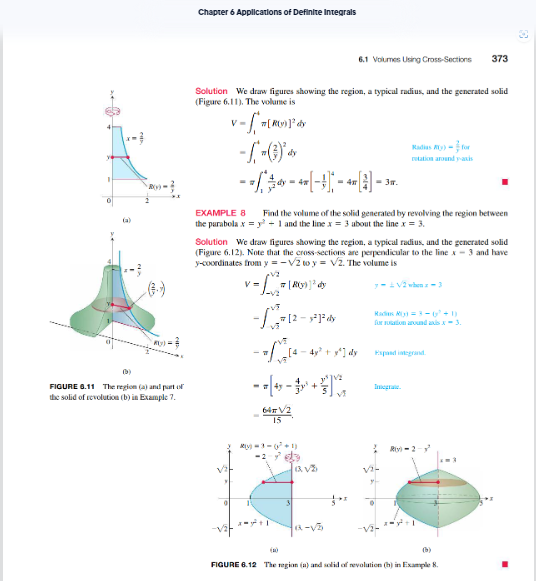
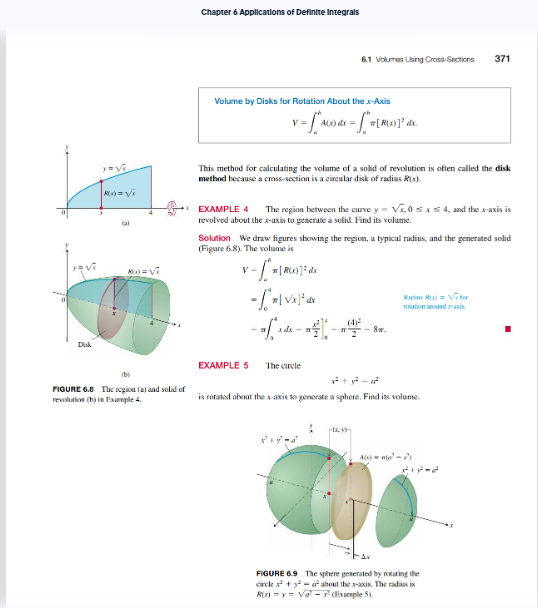
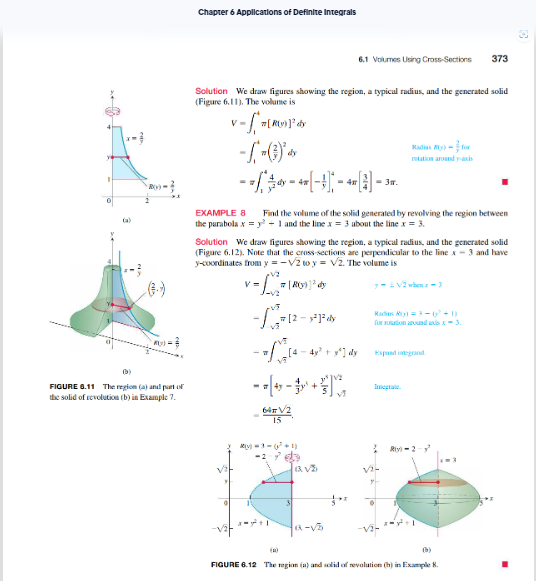
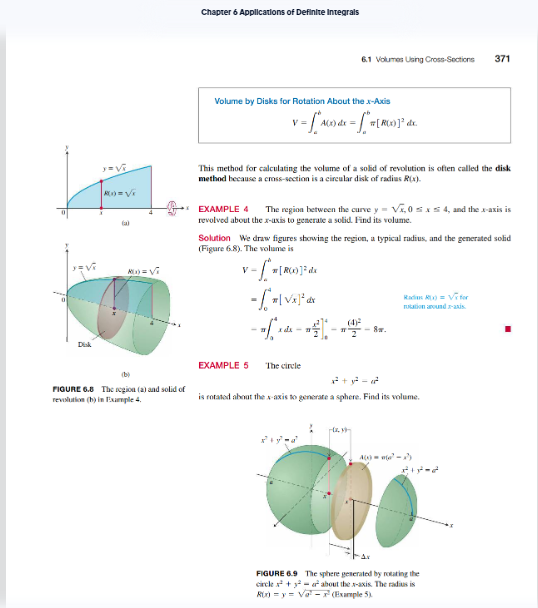
Exercise 1. Read the introduction to the subsection "Slicing bv Parallel Planes" lp. 369}. Summarize the Riemann sum argument that results in the formula in this subsection. Do not just state the formula here. Describe the geometric slices in detail for this and the ideas behind the formula. Figures 6.3 and 6.4 in the margins mav help with this. while this argument applies to many tvpes of solids, we will focus specifically,r on solids of revolution for the sake of consistencv. The disk and washer methods are specialized versions of this method. Example 4 [p. 331] is a good first example of how to use the disk method. Take a look at Figure 6.6 in the margin.The region of rEvc-lution on top is useful as an aid for understanding the solid and how to setup the integral for the volume. Notice the circular arrow wrapped around the xaxis. This is used to indicate the line of revolution and will be important when we start changing that line. Also, take a look at the red line used to indicate a cross-sectional "slice" of the solid. This is an important visual aid for un derstanding the relationship between the graph and the formula for the volume. Exercise 2. Read Example 4 [p. 3? 1} and Example T [p. 3T1 333]. Notice the different variables used betvveen these two examples. Explain how we can tell which variable to use based on the descriptions of the solids. Pay special attention to the word "about" in each statement. This last issue with the variables will become more involved when we deal with the nExt section. This is one of the major issues that comes up when setting these problems up, so it's worth considering oarefullv. Graphing the ED regions of revolution will be required for us. 1Il'llhile we won't be graphing in 3D. it is quite useful to visualixe the solids of revolution in part [b] of Figure 6.6 and 6.16 from the regions of revolution in part [a]. while thev are good exam ples, be careful when reading Example 6 lp. are} and Example 3 lp. 3331. Herer we use different axes of revolution [besides the xaxis or ,v-axis], which accounts for the difference in the formula. This is sometimes confused with the set up for the washer method, so to avoid that co nfusion, we'll stick to axes of rotation that are o ne of the primarv axes {xaxis or vaxis}. Exercise 3. Read the subsection "Solids of Revolution: The Washer Method" {p. 333 335}. Explain what tvpe of solid would need to use washer method rather than the disk method