Question: section 9.8 1 Consider the following simple harmonic motion equation. What is the frequency? s({t) =7 cos &t, where t is time in seconds _
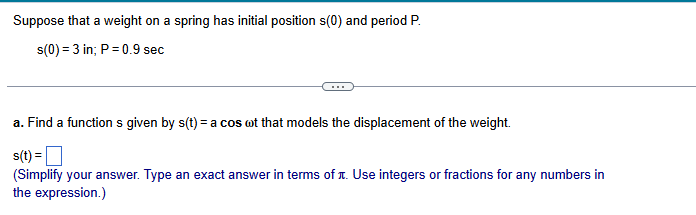


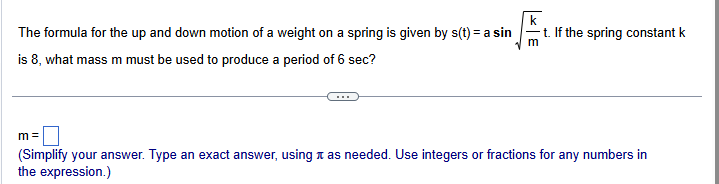


section 9.8
1
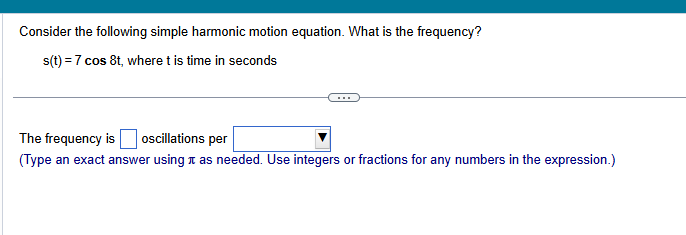
![s [E] ? s(t)=7 cos 2t, where t is time in seconds](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667ccb031fe84_467667ccb03061b9.jpg)
![(3] -0 (Simplify your answer.) Consider the following simple harmonic motion equation.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667ccb036a917_467667ccb0351fc5.jpg)
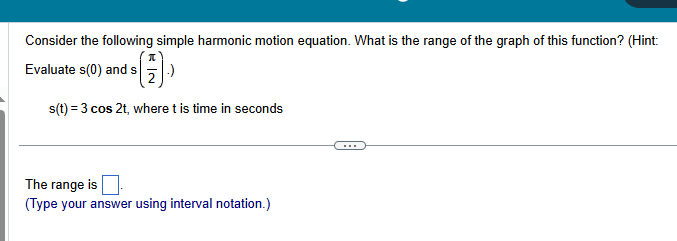
![s(0) and s [;] J s(t)=3 cos 2t, where t is time](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667ccb0421377_468667ccb040bfc2.jpg)




![weight. sty =] | (Simplify your answer. Type an exact answer in](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667ccb0604a70_469667ccb05e0852.jpg)
Consider the following simple harmonic motion equation. What is the frequency? s({t) =7 cos &t, where t is time in seconds _ - The frequency is |:| oscillations per (Type an exact answer using 1 as needed. Use integers or fractions for any numbers in the expression.) Consider the following simple harmonic motion equation. What is s(0)? s(t) =6 cos 2t, where t is time in seconds s(0) = (Simplify your answer.)T Consider the following simple harmonic motion equation. What is s [E] ? s(t)=7 cos 2t, where t is time in seconds (3] -0 (Simplify your answer.) Consider the following simple harmonic motion equation. What is the range of the graph of this function? [Hint: Evaluate s(0) and s [;] J s(t)=3 cos 2t, where t is time in seconds _ &V The range is |:| {Type your answer using interval notation.) Suppose that a weight on a spring has initial position s(0) and period P. s(0)=3in; P=09sec a. Find a function s given by s(t) = a cos wt that models the displacement of the weight. sty =] | (Simplify your answer. Type an exact answer in terms of . Use integers or fractions for any numbers in the expression.) Suppose that a weight on a spring has initial position s(0) and period P. Complete parts (a) and (b). s(0)=-5in;P=09sec _ O - (a) Find a function s given by s(t) = a cos wt that models the displacement of the weight. sit)=[ | (Simplify your answer. Type an exact answer in terms of 1. Use integers or fractions for any numbers in the expression.) Find the amplitude, period, and frequency of the simple harmonic motion of a particle moving uniformly around a circle of radius 3 units, with angular speed 6 radians per second. The amplitude is |:| units. (Simplify your answer.) { k The formula for the up and down motion of a weight on a spring is given by s(t) = a sin t. If the spring constant k is 8, what mass m must be used to produce a period of & sec? m=[ | (Simplify your answer. Type an exact answer, using x as needed. Use integers or fractions for any numbers in the expression.) The height attained by a weight attached to a spring is s{t)= 4 cos 4t inches after t seconds. Determine the maximum height the weight rises above the equilibrium position, the frequency and period of the oscillation, and when the weight first reaches its maximum height. | 9 _ What is the maximum height that the weight rises above the equilibrium position? |:|in Aweight attached to a spring is pulled down 2 inches below the equilibrium position. Complete parts (a) and (b) below. _ 1 (a) Assuming the period is 3 second, determine a trigonometric model that gives the position of the weight at time t seconds. sit)=[ | (Simplify your answer. Type an exact answer, using x as needed.)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


