Section B: Solution to Heat Conduction Problem

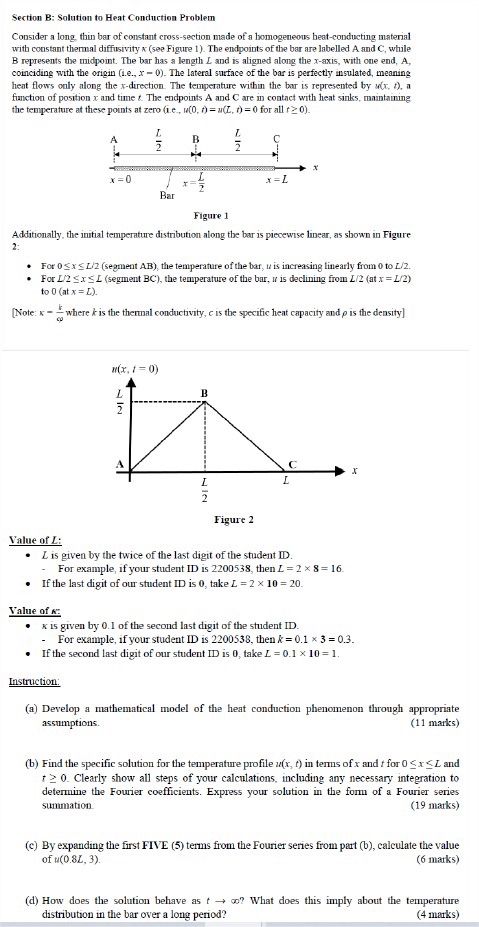
Consider a long, thin bar of constant cross$-$section made of a bomogeneons heat$-$conducting material

with constant thermal diffusivity $($see Figure $1).$ The endpoints of the bar are labelled A and $C,$ while

B represents the midpoint. The bar has a length $L$ and is aligned along the $x-$axis, with one end, A $,$

coinciding with the origin $($i$.$e$.,x-0).$ The lateral surface of the bar is perfectly insulated, meaning

heat flows only along the $x-$direction. The temperature within the bar is represented by $u(t,t),$ a

function of position $x$ and time $t.$ The endpoints A and C are in contact with heat sinks$,$ maintaining

the temperature at these points at zero $($i$.$e$,w(0,t)=u(L,t)=0$ for all $t0).$

Additionally, the initial temperature distribution along the bar is piecewise linear, as shown in Figure

$2$:

For $0x\frac{L}{2}($segment $AB),$ the temperature of the bar, $u$ is increasing linearly from $0$ to $\frac{L}{2}.$

For $\frac{L}{2}xL($segment $BC),$ the temperature of the bar, in is declining from $\frac{L}{2}($at $x=\frac{L}{2})$

to at $x=L.$

$[$Note: $-\frac{k}{}$ where $k$ is the thermal conductivity, $c$ is the specific heat capacity and $$ is the density$]$

Value of $L$ :

$L$ is given by the twice of the last digit of the student ID$.$

For example, if your student ID is $2200538,$ then $L=28=16.$

If the last digit of our student ID is $0,$ take $L=210=20.$

Value of $$ :

$K15$ given by $0\mathrm{.}1$ of the second last digit of the student ID$.$

For example, if your student ID is $2200538,$ then $k=0\mathrm{.}13=0\mathrm{.}3.$

If the second last digit of our student ID is $0,$ take $L=0\mathrm{.}110=1.$

Instruction:

$($a$)$ Develop a mathematical model of the heat conduction phenomenon through appropriate

assumptions.

$(11$ marks$)$

$($b$)$ Find the specific solution for the temperature profile $u(x,t)$ in temms of $x$ and $t$ for $0xL$ and

$t0.$ Clearly show all steps of your calculations, including any necessary integration to

determine the Fourier coefficients. Express your solution in the form of a Fourier series

summation.

$(19$ matks$)$

$($c$)$ By expanding the first FIVE $(5)$ terms from the Fourier series from part $($b$),$ calculate the value

of $u(0\mathrm{.}8L,3).$

$($d$)$ How does the solution behave as $t?$ What does this imply about the temperature

distribution in the bar over a long period?

$(4$ marks$)$