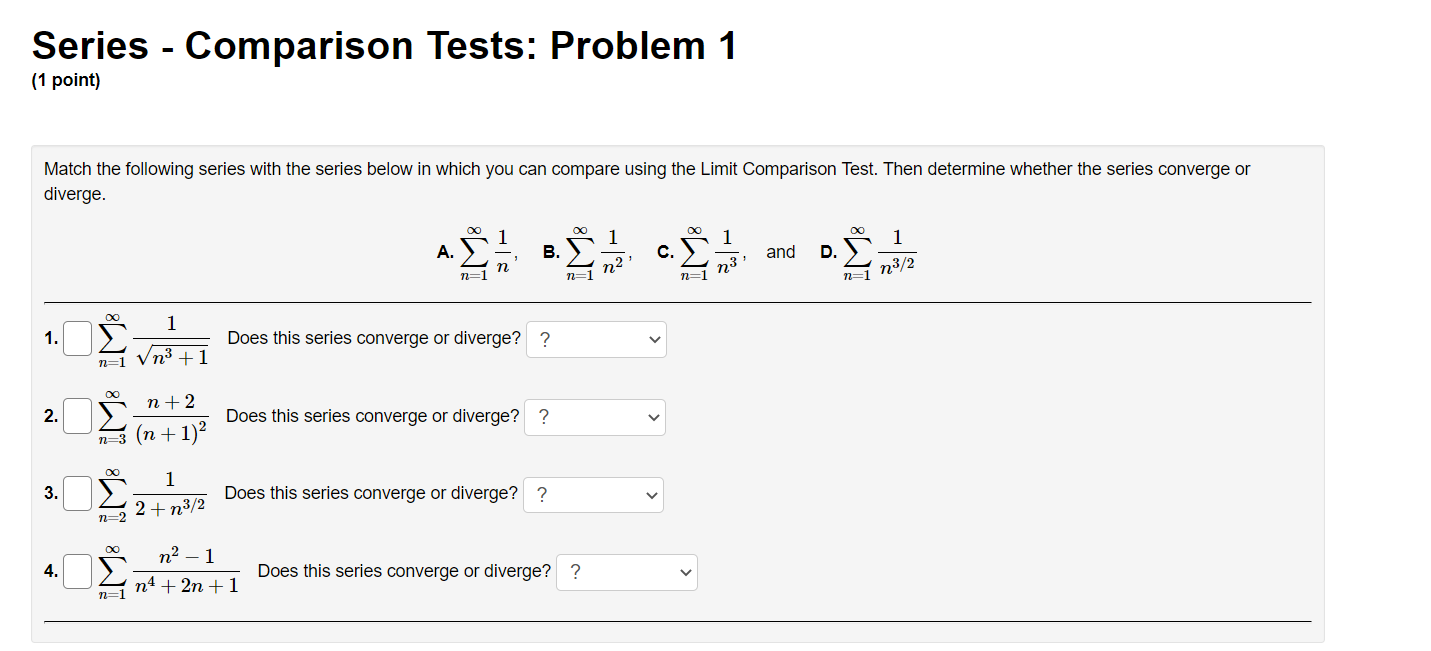
Question: Series - Comparison Tests: Problem 1 (1 point) Match the following series with the series below in which you can compare using the Limit Comparison

![i ,_1 1. C] 7 Does this series converge or diverge? ?](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6672855ed6155_2786672855eb149b.jpg)
![v "=1 113 + 1 00 n 2 2. E] 2 ;2](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6672855f43dd0_2796672855f24646.jpg)
![Does this series converge or diverge? '? v 1 3. E] Z](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6672855fbbc9f_2796672855f9566e.jpg)

![7 1 n . . . 4. E] Z Does this series](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667285604b2cc_2806672856037f06.jpg)


![? v _ n2 W n + l m] \"0 1 2.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667285624f2a5_2826672856231638.jpg)
![n2] 1 3. D Z 7 Does this series converge or diverge?](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667285631b3f2_28266728562dfc79.jpg)

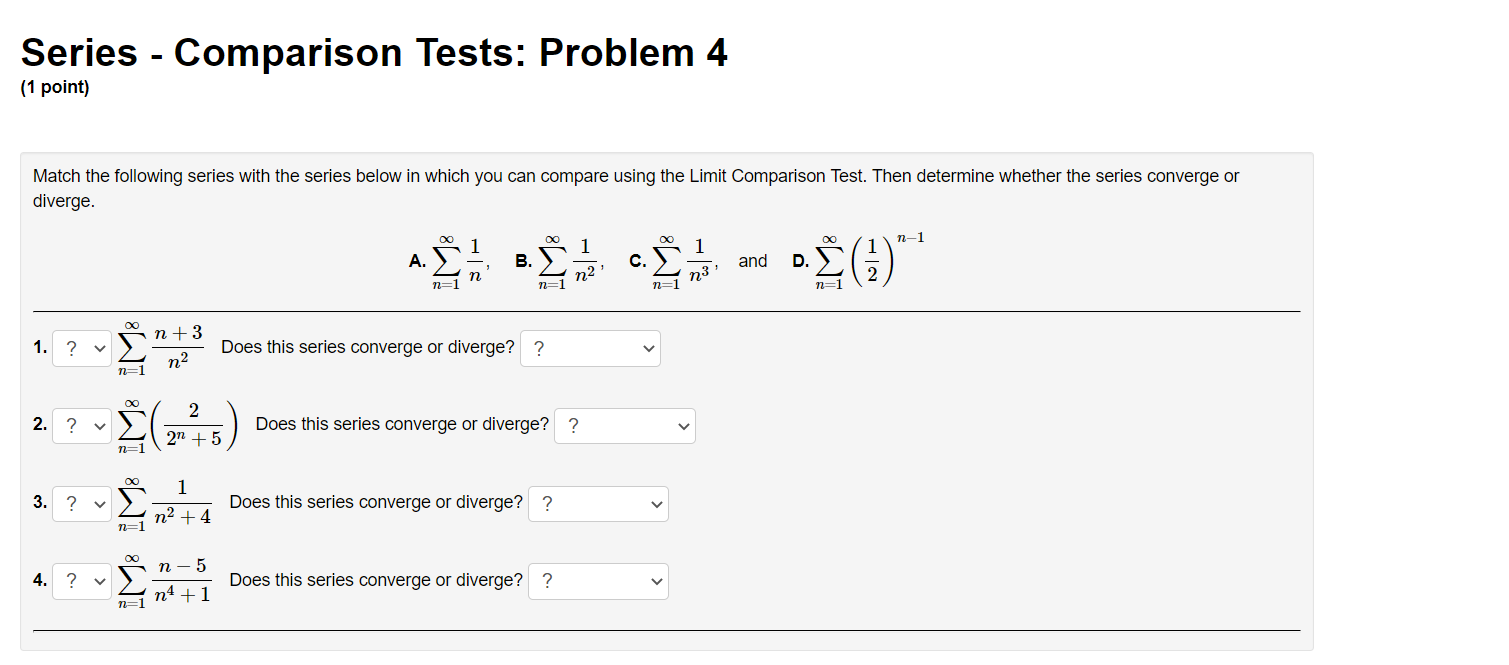
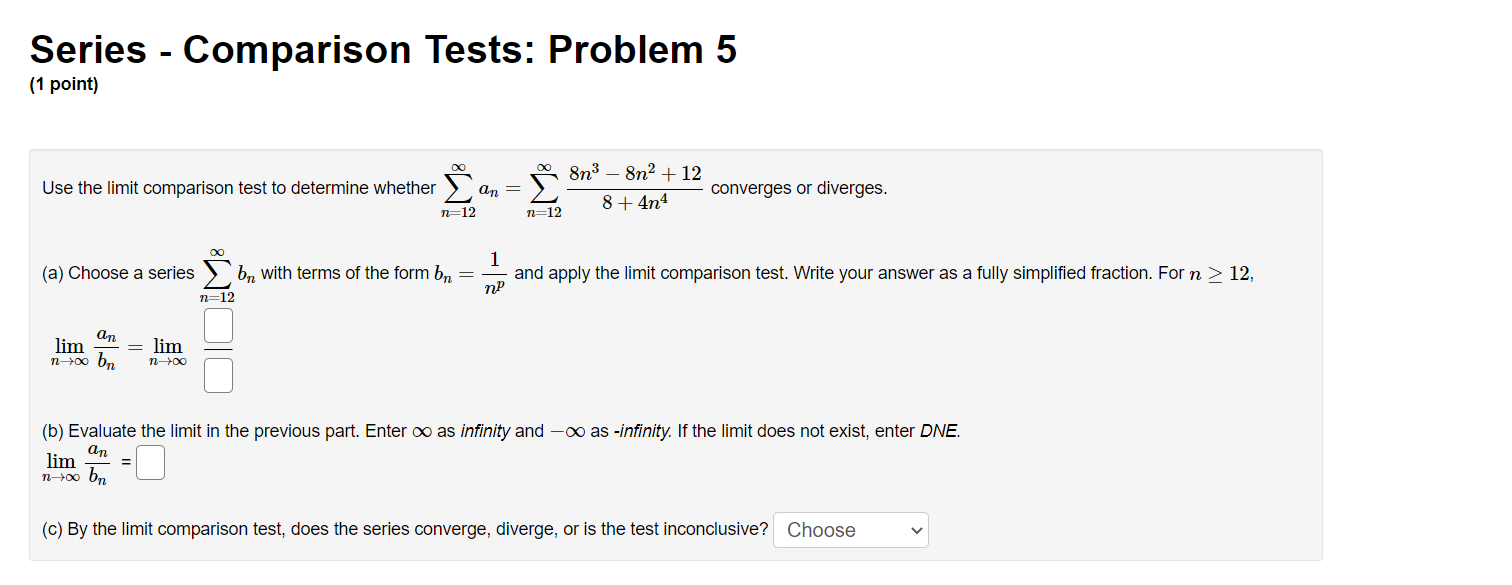
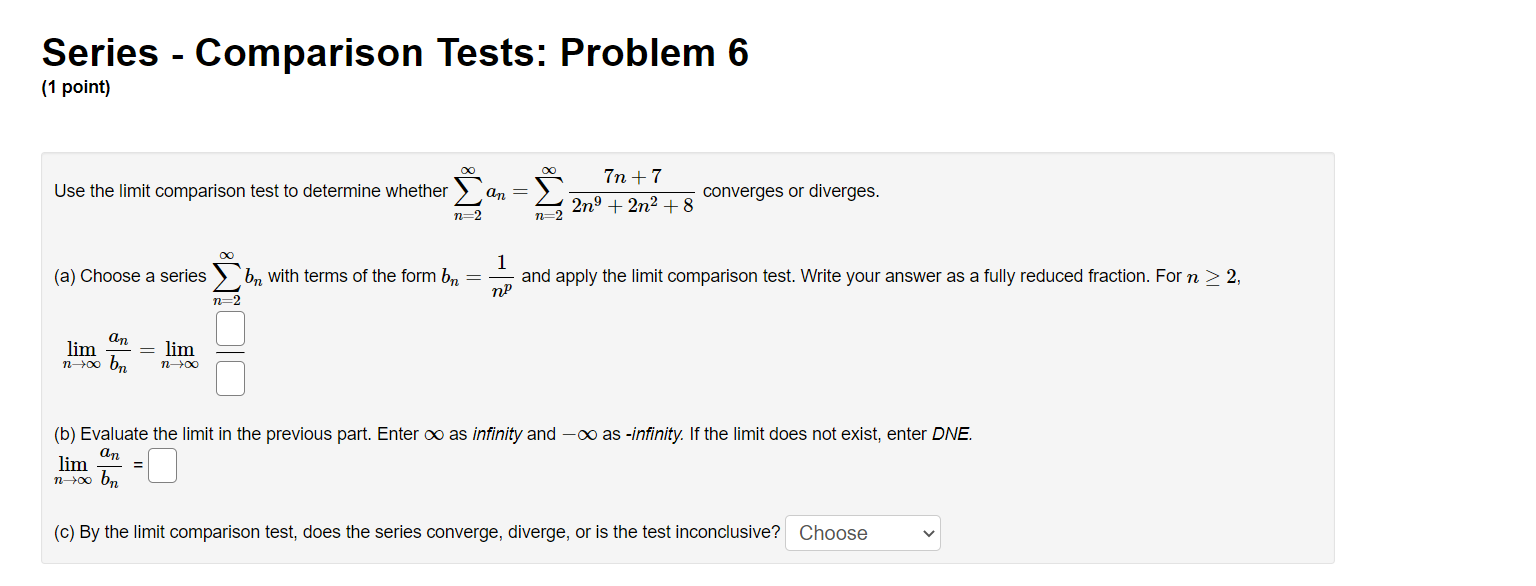


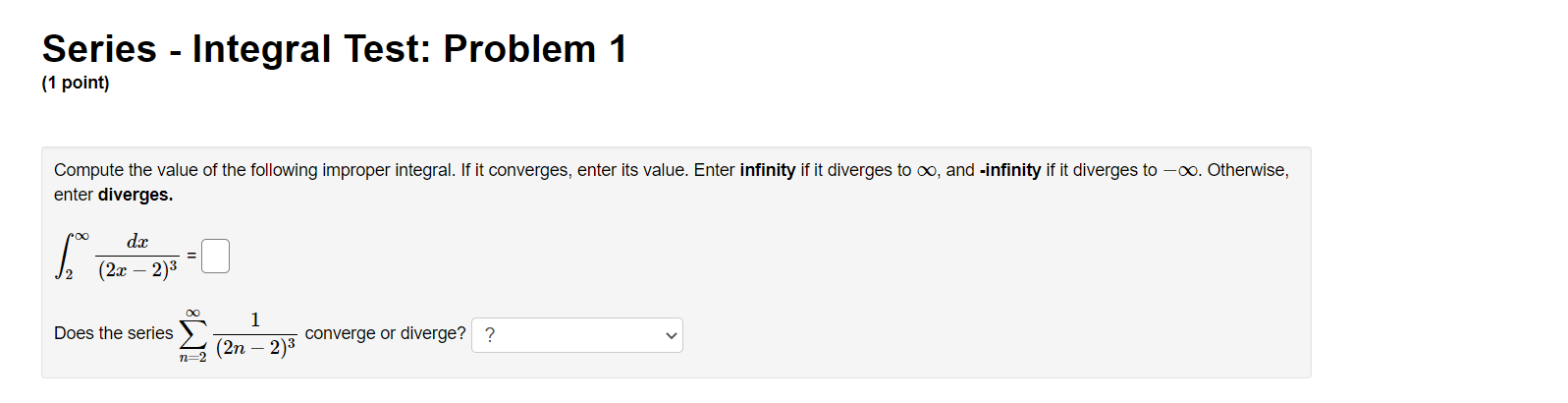
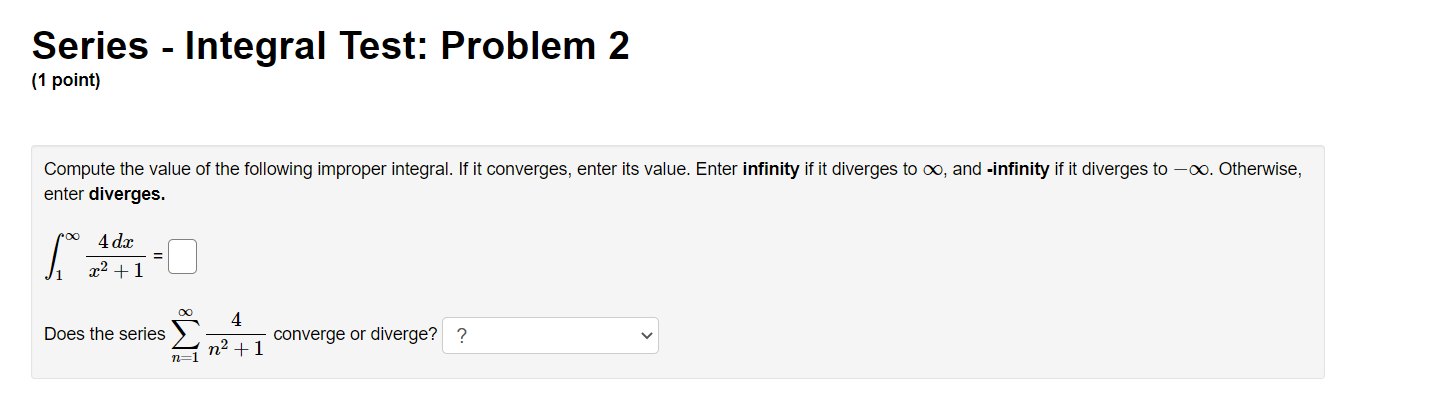
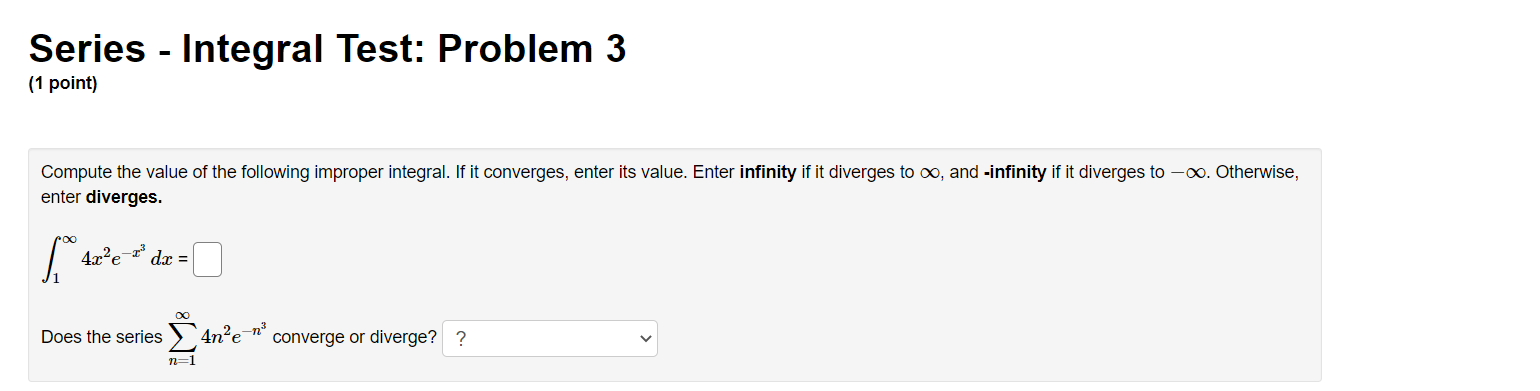
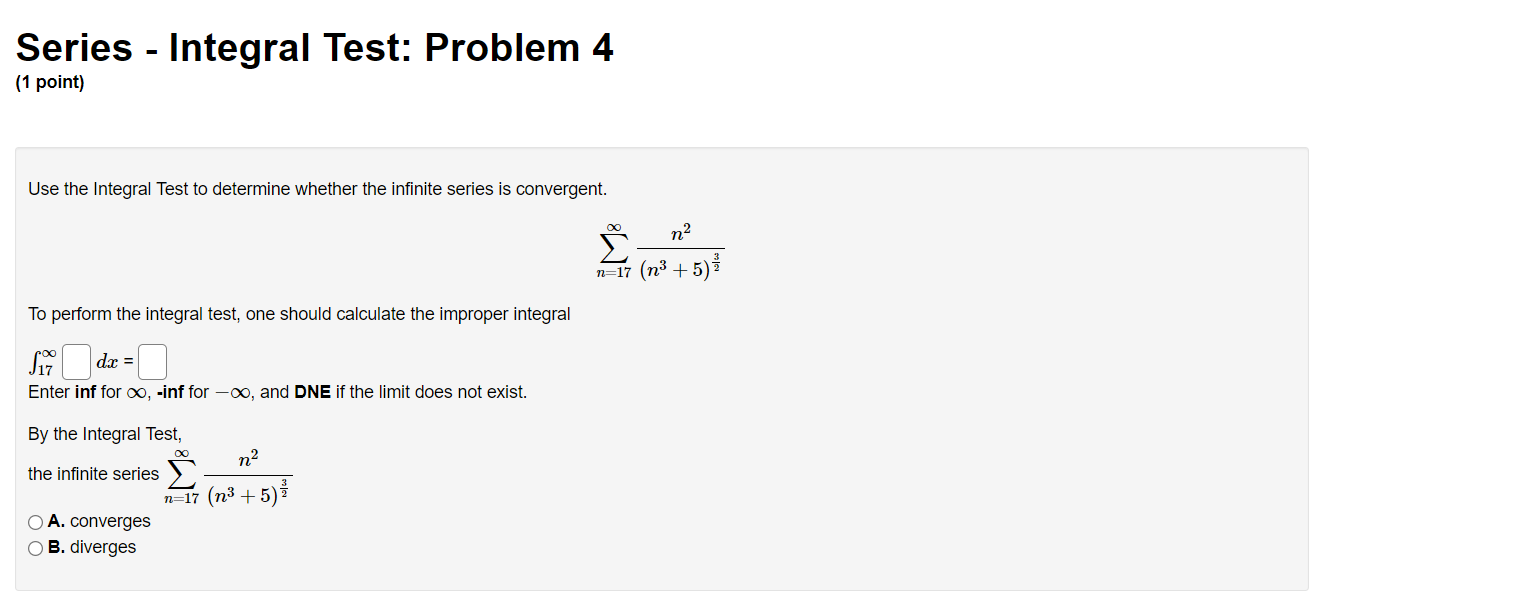


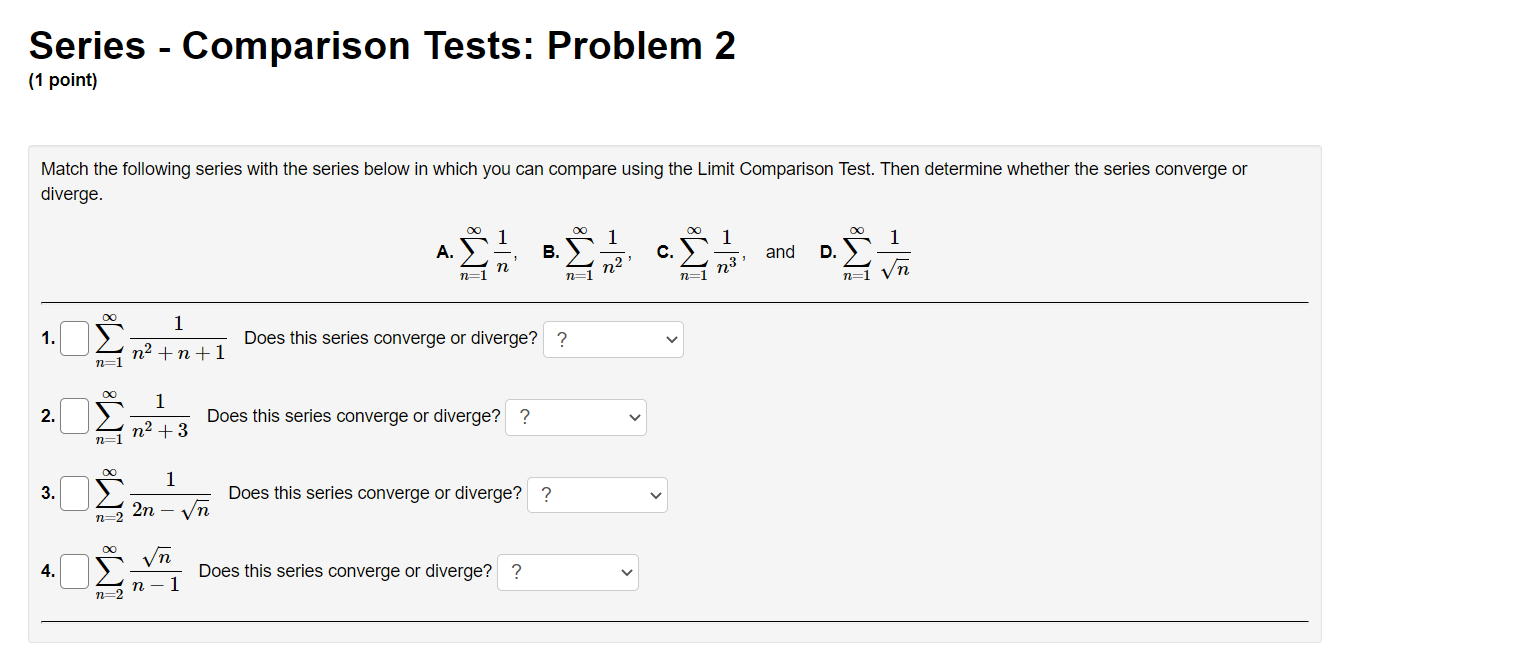
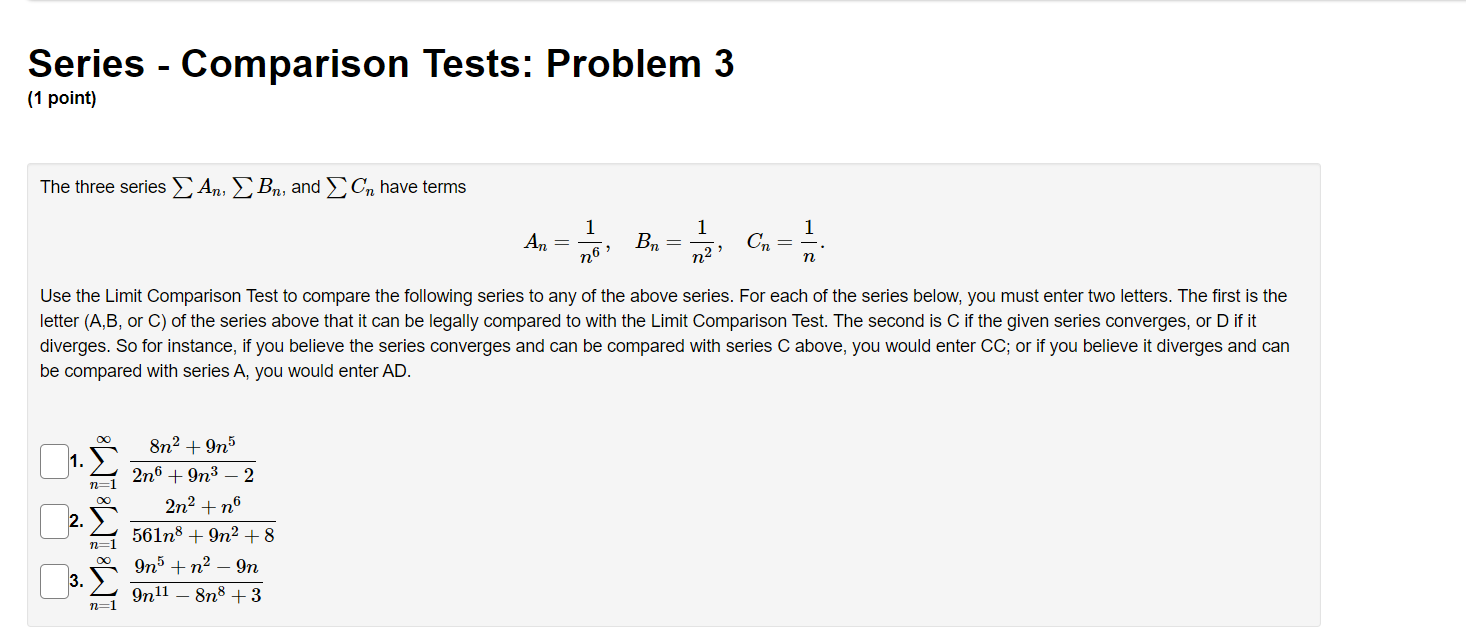
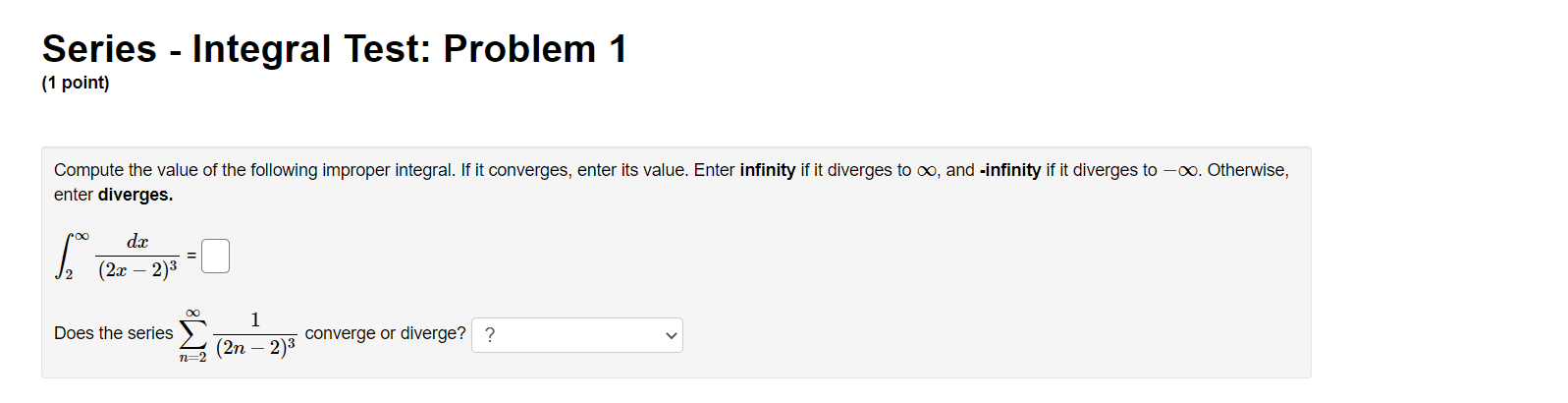
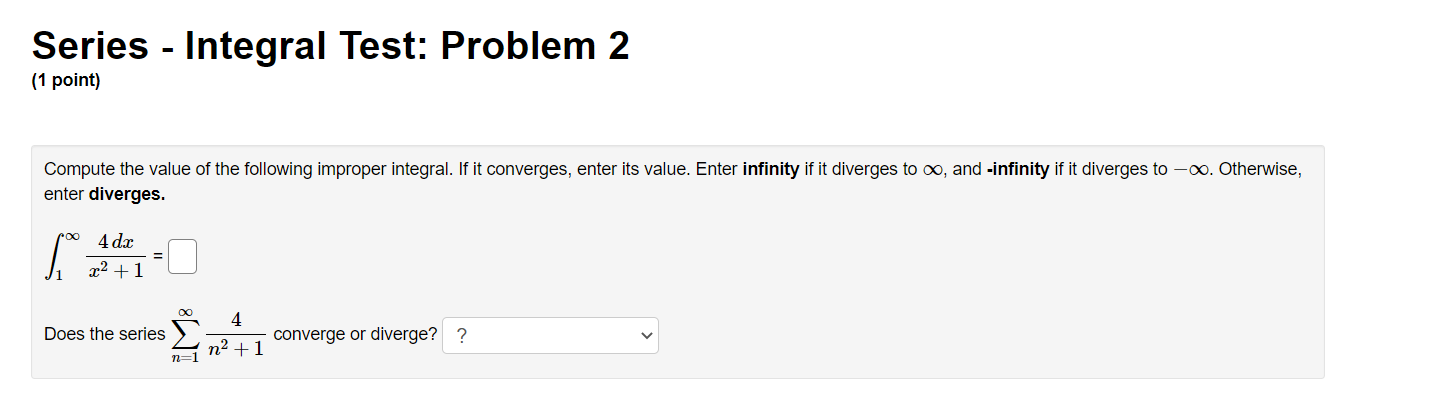
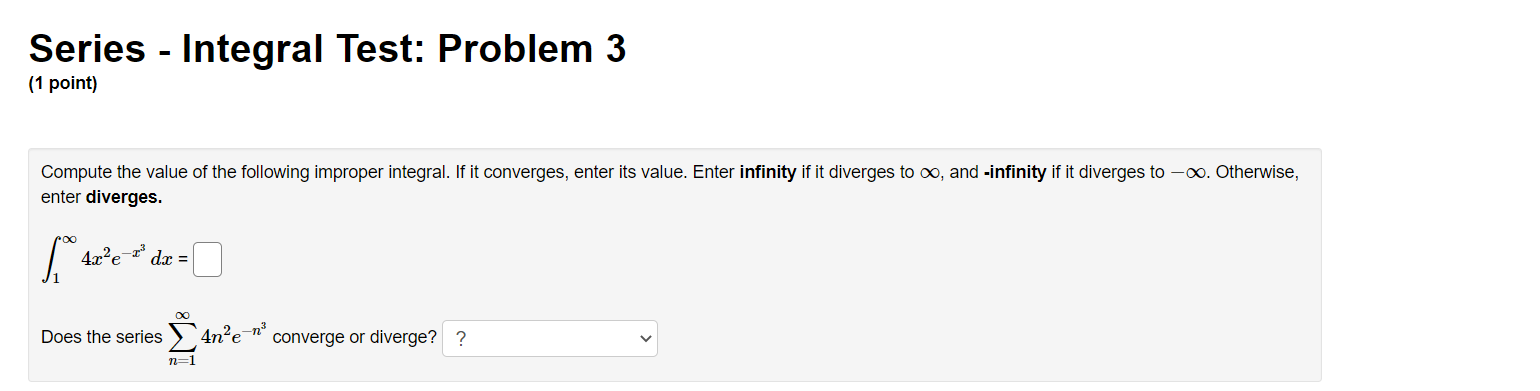
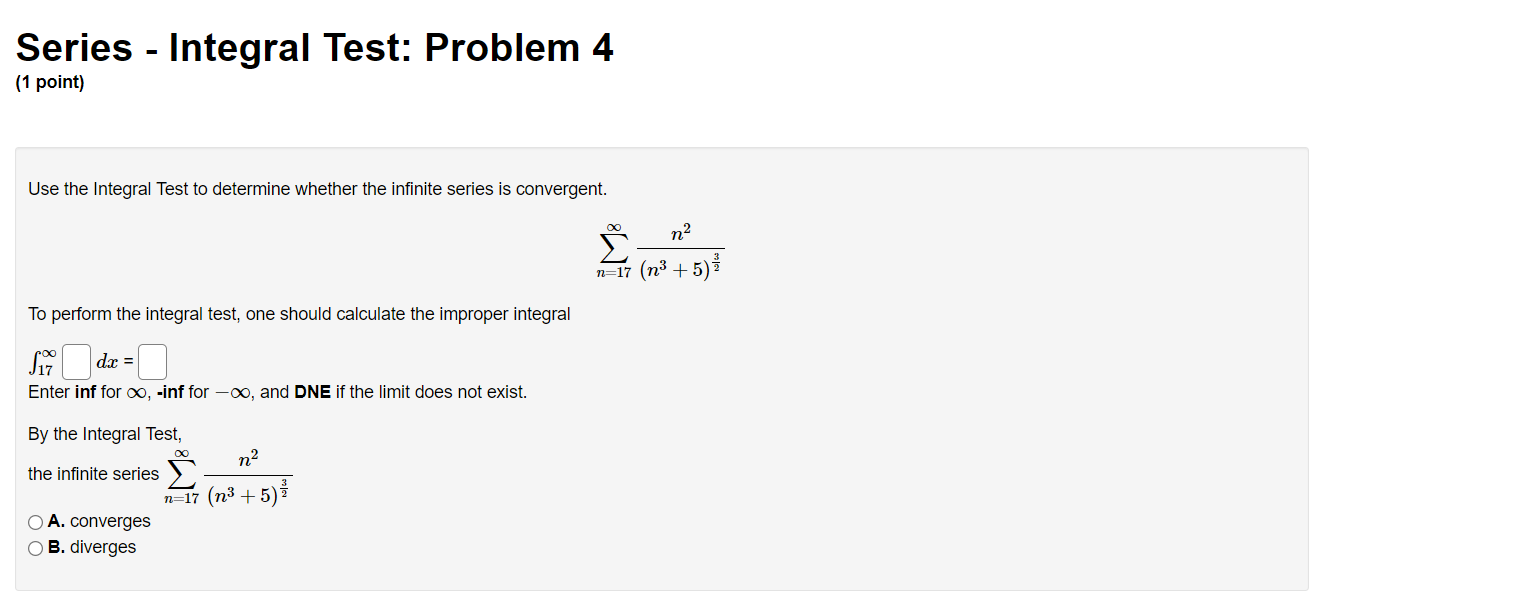
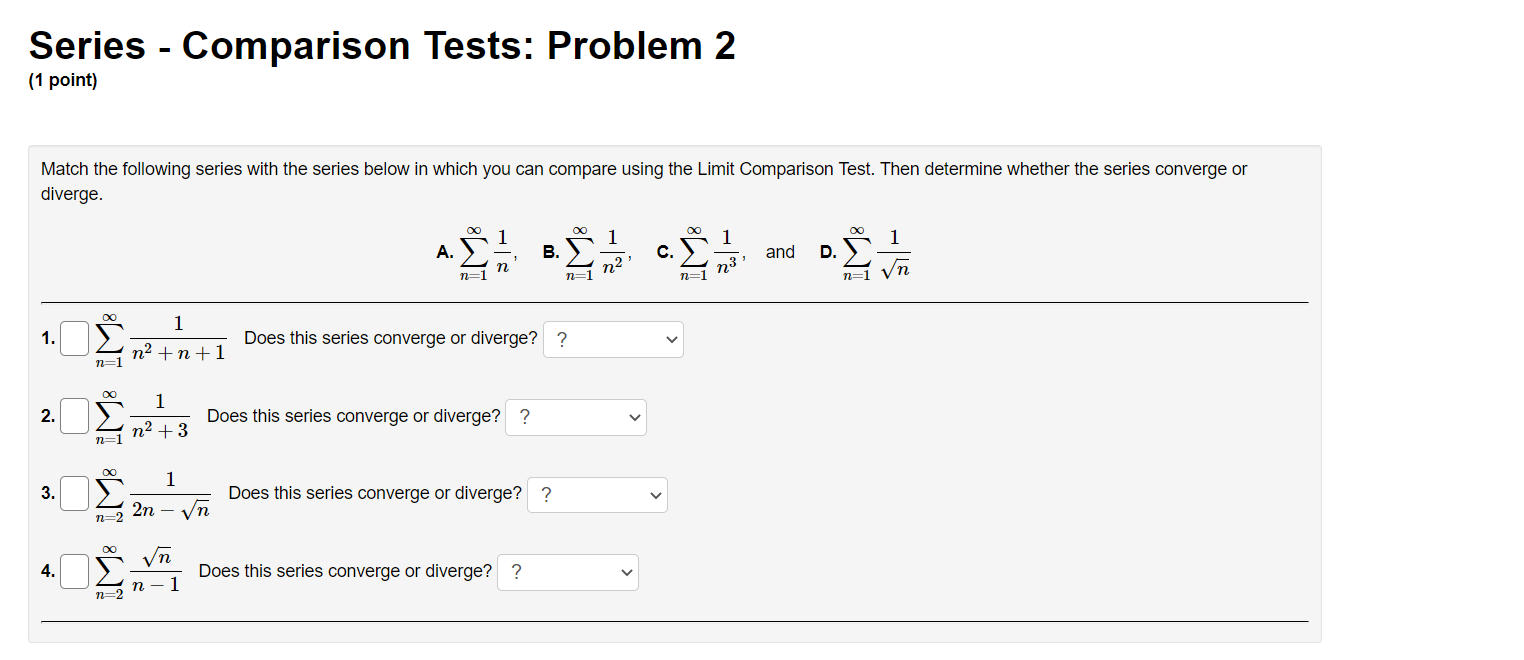
Series - Comparison Tests: Problem 1 (1 point) Match the following series with the series below in which you can compare using the Limit Comparison Test. Then determine whether the series converge or diverge. l 1 1 l A. i, B. 7, c. 7, and D. 7 i ,_1 1. C] 7 Does this series converge or diverge? ? v "=1 113 + 1 00 n 2 2. E] 2 ;2 Does this series converge or diverge? '? v 1 3. E] Z W Does this series converge or diverge? ? v n:2 oo 2 7 1 n . . . 4. E] Z Does this series converge or diverge? ? v n4 + 2n + 1 Series - Comparison Tests: Problem 2 (1 point) Match the following series with the series below in which you can compare using the Limit Comparison Test. Then determine whether the series converge or diverge. A. i, B. i, C. i, and D. 7 11:1 11, 11:1 \"2 11:1 \"'3 \"=1 31 \"0 l 1. D Z Does this series converge or diverge? ? v _ n2 W n + l m] \"0 1 2. D 2 Does this series converge or diverge? ? v n2 3 n2] 1 3. D Z 7 Does this series converge or diverge? ? v P2 211 7: [)0 1i. 4. D Z L Does this series converge or diverge? ? v n 1 Series - Comparison Tests: Problem 3 (1 point) The three series 2: A\Series - Comparison Tests: Problem 3 (1 point) The three series 2 A\Series - Comparison Tests: Problem 4 (1 point) Match the following series with the series below in which you can compare using the Limit Comparison Test. Then determine whether the series converge or diverge. co 1 DO 1 co 1 no 1 1:71 AXE, 32$, 02?, and n.2(5) n21 n21 n:1 n:1 {X} n 3 1. '3 v Z J; Does this series converge or diverge? ? v \":1 n 2 2. '3 v 2 Does this series converge or diverge? '2 v 2\" + 5 \"=1 00 3. '2 v Z 2 Does this series converge or diverge? ? v n, + 51:1 \"0 7 5 4 '3 v Does this series converge or diverge? ? v n4 + 1 Series - Comparison Tests: Problem 5 (1 point) '30 8113 811.2 + 12 _ Z converges or dlverges. 00 Use the limit comparison test to determine whether Z an : 8 + 4 4 n H.212 n:]2 00 (a) Choose a series 2: b\" with terms of the form b" = 5 and apply the limit comparison test. Write your answer as a fully simplied fraction. For n 2 12, n:12 hmzum g b\" C] (b) Evaluate the limit in the previous part. Enter 00 as innity and oo as -lnnltv If the limit does not exist, enter DNE. . an hm = C] fly)m bu (c) By the limit comparison test, does the series converge, diverge, or is the test inconclusive? Choose v Series - Comparison Tests: Problem 6 (1 point) Use the limit comparison test to determine whether in: a.n * in: 7n + 7 converges or diverges 7 211.9 + 2n2 + 8 ' \":2 \":2 (X) (a) Choose a series 2b" with terms of the form b,I = 5 and apply the limit comparison test. Write your answer as a fully reduced traction. For n. 2 2, \":2 \"rma (b) Evaluate the limit in the previous part. Enter 00 as innity and foo as -r'nn.ity. If the limit does not exist, enter DNE. . an _ 330 E ' C] (o) By the limit comparison test, does the series converge, diverge, or is the test inconclusive? Choose v Series - Comparison Tests: Problem 7 (1 point) Determine whether the following series converges or diverges: i ,9 IrFl n(n + 4)(n + 9} Input C for convergence and D for divergence: B Male: You have only one chance to enter your answer. Series - Comparison Tests: Problem 8 (1 point) Determine whether the following series converges or diverges. 8 9 n=1 n 2n Input C for convergence and D for divergence: Note: You have only one chance to enter your answer.Series - Integral Test: Problem 1 (1 point) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to co, and -infinity if it diverges to -co. Otherwise, enter diverges. dx (2ac - 2)3 1 Does the series (2n - 2)3 converge or diverge? ? 1 2Series - Integral Test: Problem 2 (1 point) Compute the value of the following improper integral. If it converges, enler its value. Enter innity if it diverges to co, and -innity if it diverges to 00. Otherwise, enler diverges. 40h: f; $2+1 =D 4 Does the series converge or diverge? ? v Series - Integral Test: Problem 3 (1 point) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to co, and -infinity if it diverges to -oo. Otherwise, enter diverges. Are ' da = [ Does the series ) 4ne-" converge or diverge? ? n= 1Series - Integral Test: Problem 4 (1 point) Use the Integral Test to determine whether the innite series is convergent. To perform the integral test, one should calculate the improper integral ff'DdFC] Enter inf for 00, -inf for 00, and DNE if the limit does not exist. By the Integral Test, \"2 (X) the innite series 2 \":17 (n3 + 5) wit 0 A. converges O B. diverges Series - Integral Test: Problem 5 (1 point) Use the Integral Test to determine whether the innite series is convergent. Fill in the corresponding integrand and the value of the improper integral. Enter inf for 00, -inf for 00, and DNE if the limit does not exist. Compare with fro C] dz = C] By the Integral Test, 00 the innite series 2: 717% n21 O A. converges O B. diverges Series - Integral Test: Problem 6 (1 point) Use the Integral Test to determine whether the innite series is convergent. m 1 \"2:;111'81 Fill in the corresponding integrand and the value of the improper integral. Enter inf for 00, -inf for 00, and DNE if the limit does not exist. Compare with 1:0 C] (in: = C] By the Integral Test, 1 n+81 00 the innite series 2: 9 O A. converges O B. diverges
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


