show excel solver, step by step please

answer for b2 and b3

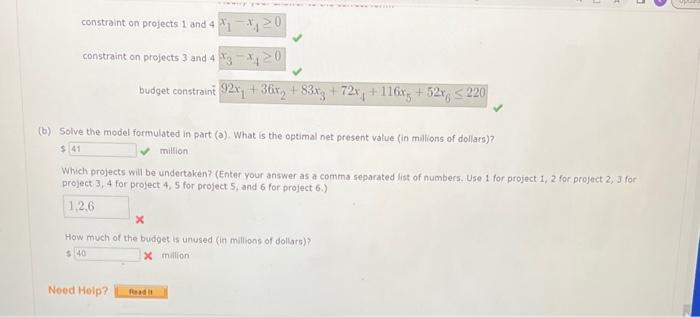
capital budgeting decision. Six real estate projects are available for investment. The net expenditures required for each project (in millions of dollars) are as follows. There are conditions that limit the investment alternatives: - At least two of projects 1, 3,5, and 6 must be undertaken - If either project 3 or 5 is undertaken, they must both be undertaken. - Project 4 cannot be undertaken unless both projects 1 and 3 also are undertaken. The budget for this investment period is $220 million. (a) Formulate a binary integer program that will enable BDC to find the projects to invest in to maximize net present value, while satistying all project restrictions and not exceeding the budget. (Let xj={1ifproject/isundertakenfori=1,2,3,4,5,6.Giveyourobjectivefunctionin0otherwise millions of doliars.) constraint on projects 1 and 4x1x40 constraint on projects 3 and 4x3x40 budget constraint 92x1+36x2+83x3+72x4+116x5+52x6220 (b) Solve the model formulated in part (a). What is the optimal net present value (in milions of dollars)? million Which projects will be undertaken? (Enter vour answer as a comma separated list of numbers. Use 1 for project 1,2 for project 2,3 for: project 3,4 for project 4 , 5 for project 5 , and 6 for project 6 .) How much of the budget is unused (in milions of dollars)? x milition capital budgeting decision. Six real estate projects are available for investment. The net expenditures required for each project (in millions of dollars) are as follows. There are conditions that limit the investment alternatives: - At least two of projects 1, 3,5, and 6 must be undertaken - If either project 3 or 5 is undertaken, they must both be undertaken. - Project 4 cannot be undertaken unless both projects 1 and 3 also are undertaken. The budget for this investment period is $220 million. (a) Formulate a binary integer program that will enable BDC to find the projects to invest in to maximize net present value, while satistying all project restrictions and not exceeding the budget. (Let xj={1ifproject/isundertakenfori=1,2,3,4,5,6.Giveyourobjectivefunctionin0otherwise millions of doliars.) constraint on projects 1 and 4x1x40 constraint on projects 3 and 4x3x40 budget constraint 92x1+36x2+83x3+72x4+116x5+52x6220 (b) Solve the model formulated in part (a). What is the optimal net present value (in milions of dollars)? million Which projects will be undertaken? (Enter vour answer as a comma separated list of numbers. Use 1 for project 1,2 for project 2,3 for: project 3,4 for project 4 , 5 for project 5 , and 6 for project 6 .) How much of the budget is unused (in milions of dollars)? x milition