Question: Show that B = {A1, A2, A3} is a basis for U. Any matrix of the form X T X is symmetric. If X ?
- Show that B = {A1, A2, A3} is a basis for U.
- Any matrix of the form XTX is symmetric. If X ? M2(R) has columns u, v, i.e., X = u v , find [XTX]B in terms of u u, v v, and u v
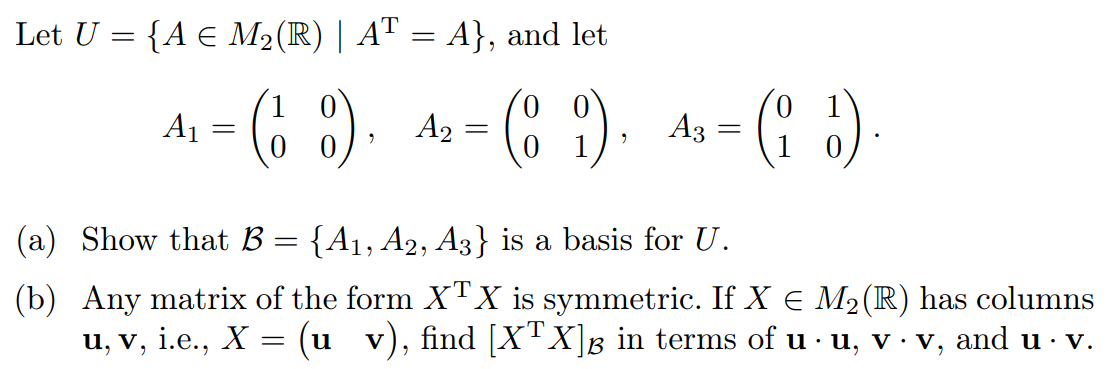
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


