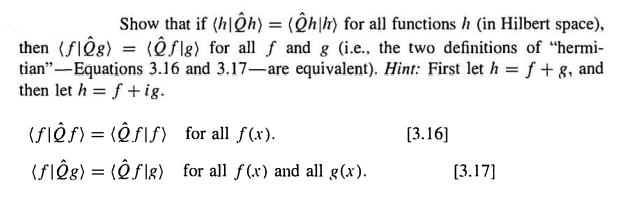
Show that if (h|h) = (h\h) for all functions h (in Hilbert space), then (flg) = (flg) for all f and g (i.e., the two definitions of "hermi- tian"-Equations 3.16 and 3.17-are equivalent). Hint: First let h = f+ 8, and then let h = f +ig. (SIF) = (FIS) for all f(x). [3.16] (FIg) = ( \g) for all f(x) and all g(x). [3.17]