Question: . Show that the function d : S x S - R is positive definite, i.e. d(a, b) =0 - a=b and symmetric d(a, b)

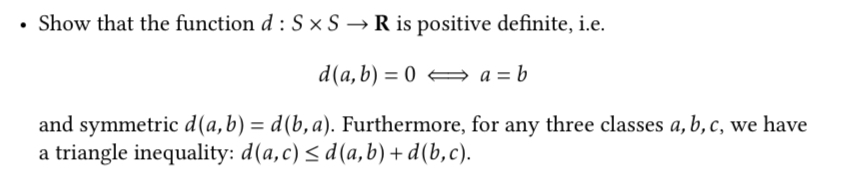
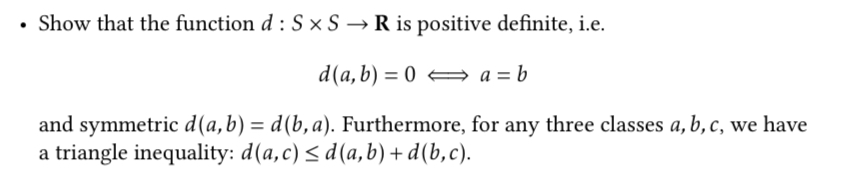
. Show that the function d : S x S -

. Show that the function d : S x S - R is positive definite, i.e. d(a, b) =0 - a=b and symmetric d(a, b) = d(b, a). Furthermore, for any three classes a, b, c, we have a triangle inequality: d(a, c)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Show the parse trees for the two parses that the grammar assigns for sentence S1. S1: the train station bus rumbles [3 marks] (b) Give an algorithm for a bottom-up passive chart parser without...

software projects failed. In the run-up to Y2K, most of the world's large companies claimed that fixing the Millennium Bug was a large project whose success was critical to their survival. One would...

350 Specification and Verification II Explain how a register can be modelled either as a unit-delay, or with an explicit clock input. [4 marks] Describe the relationship between the two models. [4...

HERE ARE MY QUESTIONS Question 4 A game G = (N. S, u) is said to be symmetric if S1 = $2 = ... = S,, and there is some function f : S, x S- - R such that f(s,, s_,) is symmetric with respect to the...

networsksss [4 marks] (c) Write down a HOPLA term realising the parallel composition of PCCS. Use this to give an encoding of PCCS into HOPLA, specifying a HOPLA term JPK for every PCCS term P....

This CPU scheduler initiated or resumed transaction processing 10,000 times. The total CPU usage was 25 seconds. Disc 1 made 5000 transfers with an average transfer time of 10 ms. Disc 2 made 2000...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

CS229 Problem Set #3 9 (a) [5 points] Exact marginal inference. By exploiting the linearity of f, we will first show that p(x) can be determined analytically. We shall do so by explicitly finding a...

I am struggling to do the proper computations for some simple accounting. After i get this down, i will produce a paper on the importance of each number i solved for. Can someone please help me...

OCaml Language Background: Tables A very common way of storing data for presentation or manipulation is as a table. While spreadsheet applications like Excel, Numbers, Google Sheets, and LibreOffice...

Given the following information: Petty cash fund $175 Postage stamps 58 Cash on hand 4,265 Traveler's checks 550 Checking balance, First National Bank 30,425 Checking balance, Third National Bank...

A large bakery chain is planning for its flour supply over the next three months. Its requirements are estimated at 130,000 kg, 170,000 kg, and 110,000 kg for months 1, 2 and 3, respectively. It...

Determine if each function is increasing or decreasing 7 . f ( x ) = 4 x + 3 9 . a ( x ) = 5 - 2 x 1 1 . h ( x ) = - 2 x + 4 1 3 . j ( x ) = 1 x - 3 2 1 5 . n ( x ) = - 1 x - 2 3

On January 1, 2014, Plate Company purchased a 90% interest in the common stock of Set Company for $650,000, an amount $20,000 in excess of the book value of equity acquired. The excess relates to the...

The stock of the Health Corporation is currently selling for $20 a share and is expected to pay a $1 dividend at the end of the year. If you bought the stock now and sold it for $23 after receiving...

Using the information in E10-3, assume that in July 2014, Thome Company incurs the following manufacturing overhead costs. Instructions (a) Prepare a flexible budget performance report, assuming that...

Select the best answer for each of the following. 1. On January' 1, 2015, Bay Company issues bonds with a face value of $850,000 that pay 9% interest semiannually and mature in 15 years. The market...

Identify the accounts in which each of the following transactions for Oak Leaf Furniture, a custom manufacturer of oak tables and chairs, would be debited and credited: 1. Issued oak materials into...

Write a program to wish happy birthday to a student. Firstly, take today month and day as an input and secondly take birthday as an input in the form of month and day. If the input day and month...

Citicools outstanding stock consists of (a) 40,000 shares of noncumulative 7.5% preferred stock with a $10 par value and (b) 100,000 shares of common stock with a $1 par value. During its first four...

In 2005, Randa Merchandising, Inc., sold its interest in a chain of wholesale outlets, taking the com- pany completely out of the wholesaling business. The company still operates its retail outlets....

The stockholders equity of Whiz.com at the beginning of the day on February 5 follows: On February 5, the directors declare a 20% stock dividend distributable on February 28 to the February 15...