Show that the worst case delay through a nxn array of the type shown in Figure $9\mathrm{.}6$b is $6($n$-1)-1$ gate delays, as claimed in Section $9\mathrm{.}3\mathrm{.}1,9\mathrm{.}3\mathrm{.}1$ Array Multiplier

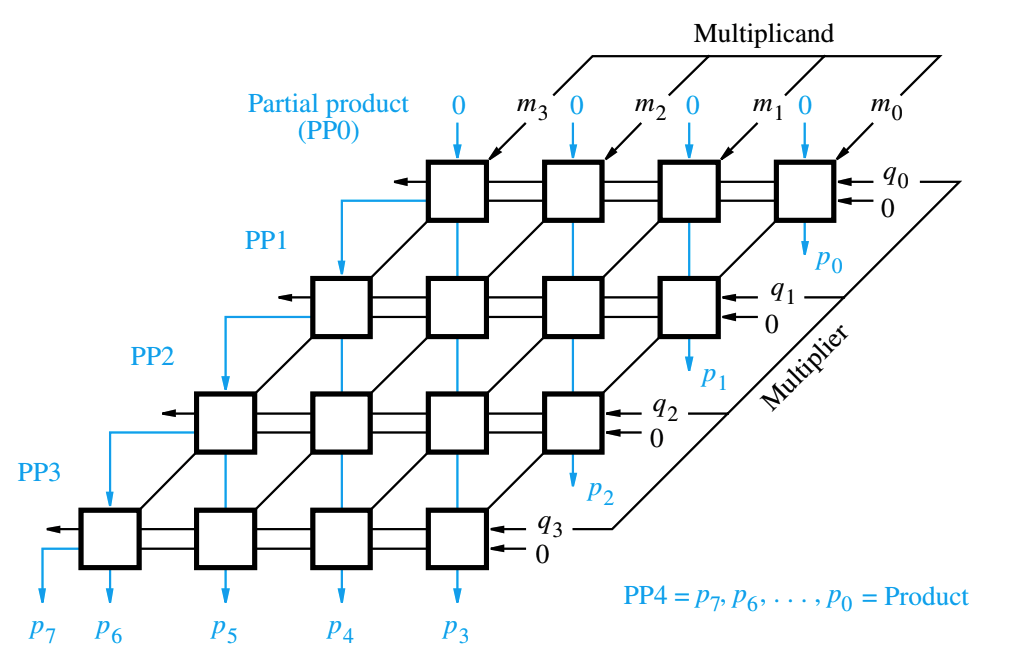
Binary multiplication of unsigned operands can be implemented in a combinational, two$-$

dimensional, logic array, as shown in Figure $9\mathrm{.}6$b for the $4-$bit operand case. The main

component in each cell is a full adder, FA$.$ The AND gate in each cell determines whether a

multiplicand bit, mj$,$ is added to the incoming partial$-$product bit, based on the value of the

multiplier bit, qi$.$ Each row i$,$ where i adds the multiplicand $($appropriately shifted$)$

to the incoming partial product, PPi, to generate the outgoing partial product, PP$($i $+1),$ if

qi $=1.$ If qi $=0,$ PPi is passed vertically downward unchanged. PP$0$ is all $0$s$,$ and PP$4$ is

the desired product. The multiplicand is shifted left one position per row by the diagonal

signal path. We note that the row$-$by$-$row addition done in the array circuit differs from the

usual hand addition described previously, which is done column$-$by$-$column.

The worst$-$case signal propagation delay path is from the upper right corner of the

array to the high$-$order product bit output at the bottom left corner of the array. This critical

path consists of the staircase pattern that includes the two cells at the right end of each row, followed by all the cells in the bottom row. Assuming that there are two gate delays

from the inputs to the outputs of a full$-$adder block, FA$,$ the critical path has a total of

$6($n $1)1$ gate delays, including the initial AND gate delay in all cells, for an n $\backslash$times n

arrray. In the first row of the array, no full adders are needed, because

the incoming partial product PP$0$ is zero. This has been taken into account in developing

the delay expression.