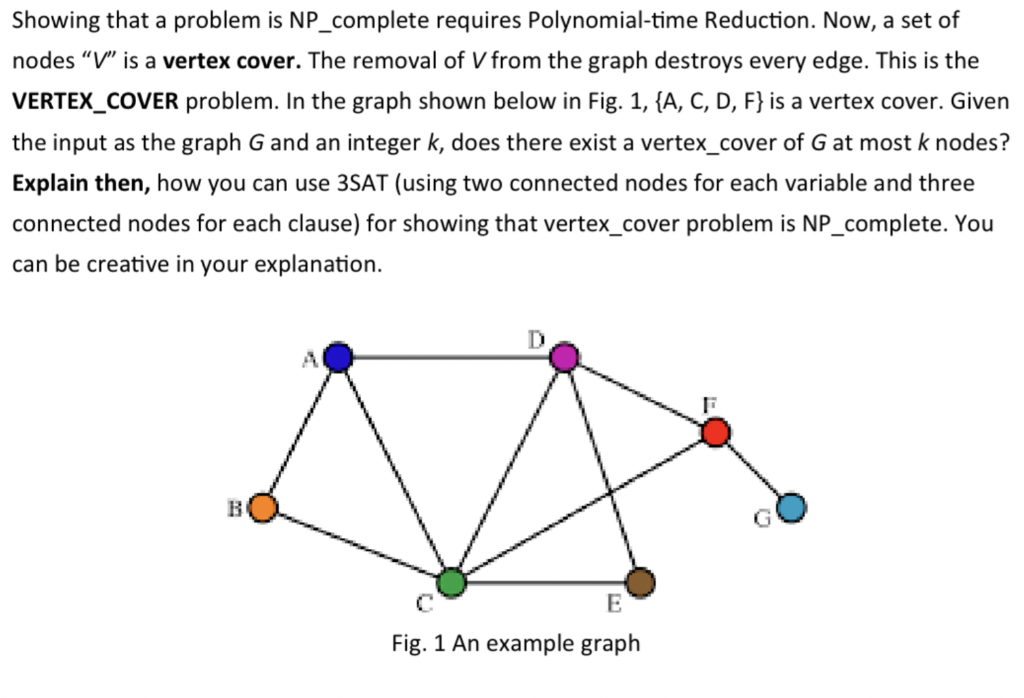
Showing that a problem is NP_complete requires Polynomial-time Reduction. Now, a set of nodes " V " is a vertex cover. The removal of V from the graph destroys every edge. This is the VERTEX_COVER problem. In the graph shown below in Fig. 1, {A,C,D,F} is a vertex cover. Given the input as the graph G and an integer k, does there exist a vertex_cover of G at most k nodes? Explain then, how you can use 3SAT (using two connected nodes for each variable and three connected nodes for each clause) for showing that vertex_cover problem is NP_complete. You can be creative in your explanation. rig. \& HIl exarrpie grapri