Simple Real Options Analysis

The problem involves a simple two$-$phase development project $($denoted as Project REOPAS$).$ All values are in millions of dollars. For the project, you may invest in the first, both or in neither phase, however,

you cannot invest in the second phase without investing in the first.

Phase $1$ requires an investment of $$200,000.$ One year later the project delivers either $$340,000$ or $$120,000$ with equal probability $($label as favorable$/$unfavorable Phase $1).$ At that time, after the Phase $1$ payout

has been received, you may invest an additional $$200,000$ for Phase $2.$ One year later, Phase $2$ pays out either $20\%$ more cash than Phase $1$ actually delivered or $20\%$ less for both favorable and unfavorable

Phase $1$ outcomes $($again each outcome is equally likely$).$ Assume no taxes and the company uses a $12\%$ per year discount rate.

Set up the required decision trees to answer the following $($indicate worksheet on which the answer was identified$)$:

a$.$ How much would the project be worth if it offered only the Phase $1$ opportunity?

b$.$ How much would Phase $2$ be worth if you had to choose today, once and for all, whether or not to invest in it $($i$.$e$.$ regardless of the outcome of Phase $1)?$

c$.$ How much is the project worth if you have access to both phases and can wait to decide whether to invest in Phase $2?$

d$.$ Determine the value of the real option presented in part c $($compared to b$,$ i$.$e$.$ committed to both phases$).$

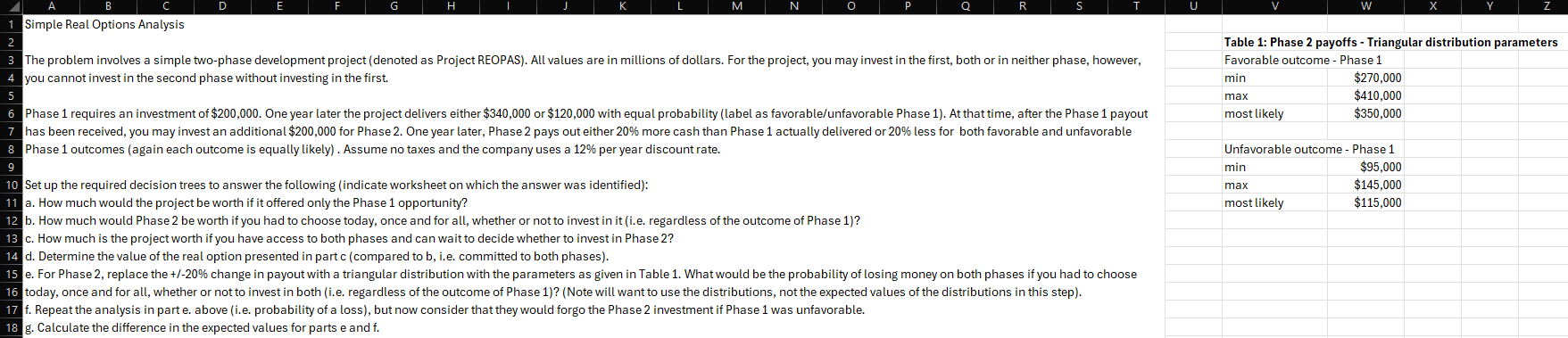
e$.$ For Phase $2,$ replace the $\frac{+}{-}20\%$ change in payout with a triangular distribution with the parameters as given in Table $1.$ What would be the probability of losing money on both phases if you had to choose

today, once and for all, whether or not to invest in both $($i$.$e$.$ regardless of the outcome of Phase $1)?($Note will want to use the distributions, not the expected values of the distributions in this step$).$

f$.$ Repeat the analysis in part e$.$ above $($i$.$e$.$ probability of a loss$),$ but now consider that they would forgo the Phase $2$ investment if Phase $1$ was unfavorable.

g$.$ Calculate the difference in the expected values for parts e and f$.$