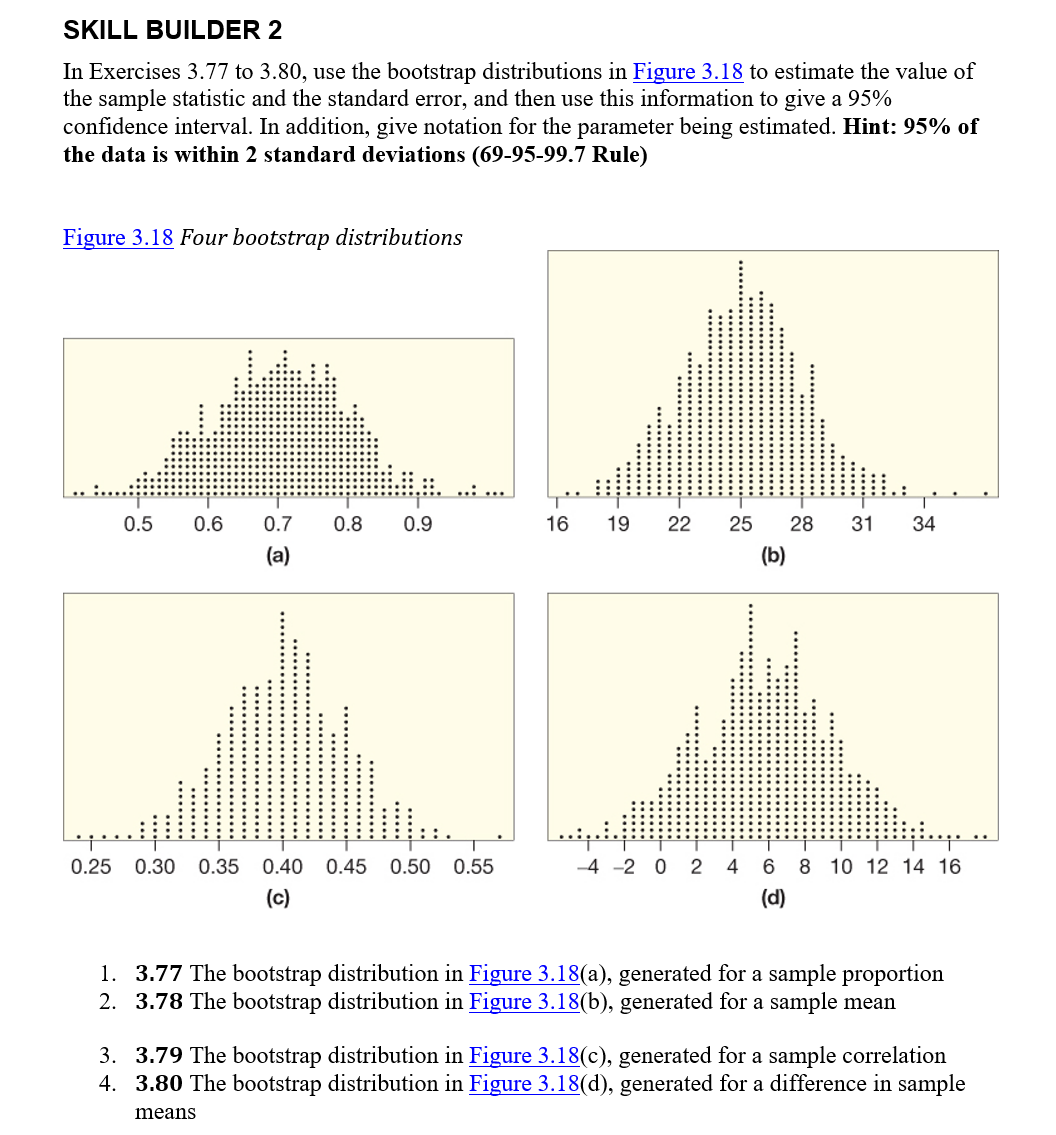
SKILL BUILDER 1 In Exercises 3.75 and 3.76, a sample is given. Indicate whether each option is a possible bootstrap sample from this original sample. 1. 3.75 Original sample: 17, 10, 15, 21, 13, 18. Do the values given constitute a possible bootstrap sample from the original sample? 1. 10, 12, 17, 18, 20, 21 2. 10, 15, 17 3. 10, 13, 15, 17, 18, 21 4. 18, 13, 21, 17, 15, 13, 10 5. 13, 10, 21, 10, 18, 17 2. 3.76 Original sample: 85, 72, 79, 97, 88. Do the values given constitute a possible bootstrap sample from the original sample? 1. 79, 79, 97, 85, 88 2. 72, 79, 85, 88, 97 3. 85, 88, 97, 72 4. 88, 97, 81, 78, 85 5. 97, 85, 79, 85, 97 6. 72, 72, 79, 72, 79 SKILL BUILDER 2 In Exercises 3.77 to 3.80, use the bootstrap distributions in Figure 3.18 to estimate the value of the sample statistic and the standard error, and then use this information to give a 95% confidence interval. In addition, give notation for the parameter being estimated. Hint: 95% of the data is within 2 standard deviations (69-95-99.7 Rule) Figure 3.18 Four bootstrap distributions 0.5 0.6 0.7 (a) 0.8 0.9 16 19 22 25 28 31 34 (b) 0.25 0.30 0.35 0.40 0.45 0.50 0.55 (c) -2 0 2 4 6 8 10 12 14 16 (d) 1. 3.77 The bootstrap distribution in Figure 3.18(a), generated for a sample proportion 2. 3.78 The bootstrap distribution in Figure 3.18(b), generated for a sample mean 3. 3.79 The bootstrap distribution in Figure 3.18(c), generated for a sample correlation 4. 3.80 The bootstrap distribution in Figure 3.18(d), generated for a difference in sample means SKILL BUILDER 3 Exercises 3.81 to 3.84 give information about the proportion of a sample that agrees with a certain statement. Use StatKey or other technology to estimate the standard error from a bootstrap distribution generated from the sample. Then use the standard error to give a 95% confidence interval for the proportion of the population to agree with the statement. StatKey tip: Use CI for Single Proportion and then Edit Data to enter the sample information. 1. 3.81 In a random sample of 100 people, 35 agree. 2. 3.82 In a random sample of 250 people, 180 agree. 3. 3.83 In a random sample of 400 people, 112 agree and 288 disagree. 4. 3.84 In a random sample of 1000 people, 382 people agree, 578 disagree, and 40 are undecided.