So as we have seen, multiple functions can have the same derivative, therefore a single derivative can have multiple antiderivatives. In fact, a single derivative has infinitely many antiderivatives. We have seen that

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}f(x)dx=F(x)+C$

This is what is known as the general antiderivative. When we are given a point on $F,$ that is when we can solve for $C$ and find the unique antiderivative meeting those criteria.

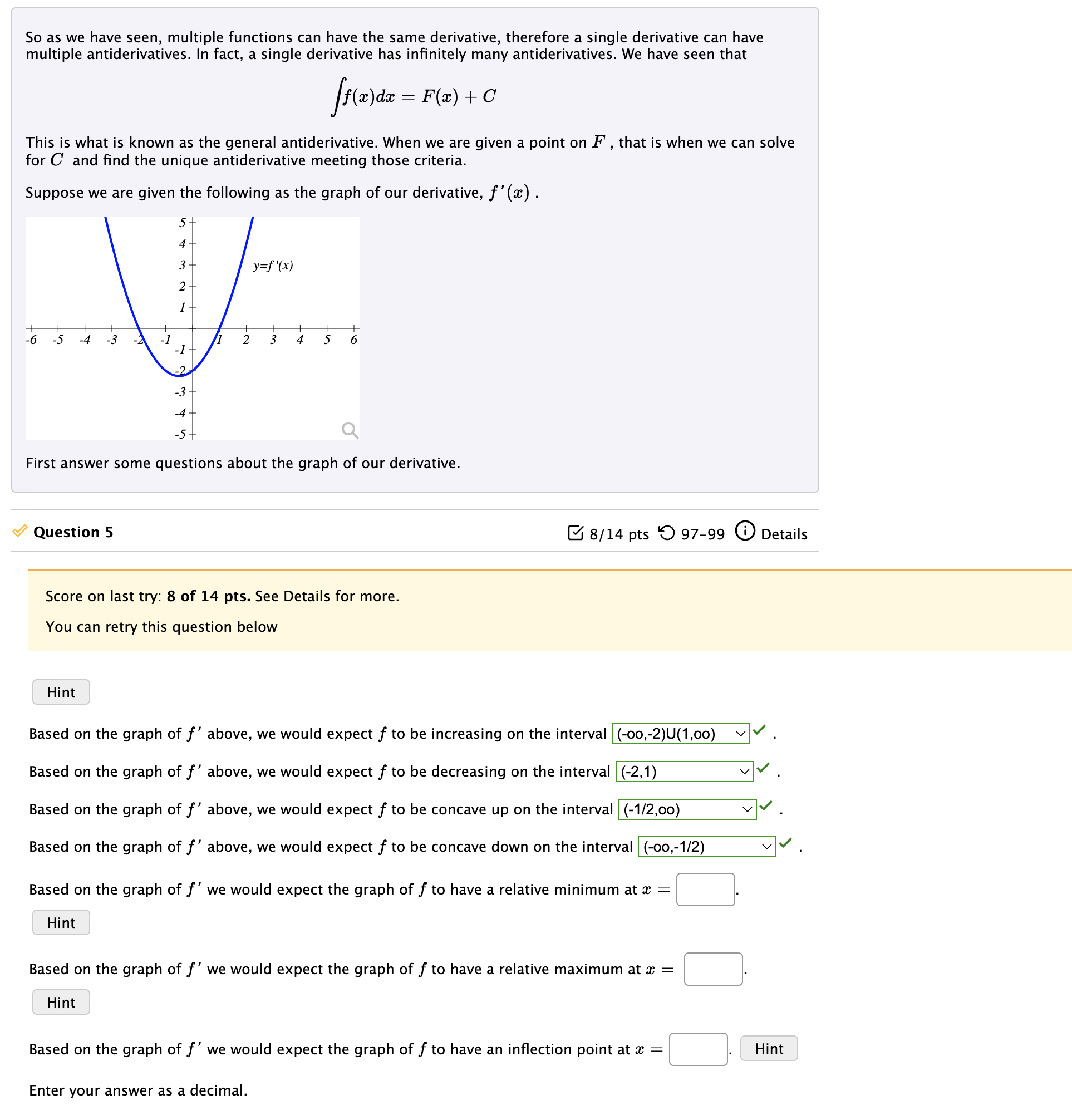
Suppose we are given the following as the graph of our derivative, $f^{\text{'}}(x).$

First answer some questions about the graph of our derivative.

Question $5$

$8/14$ pts

$97-99$

Details

Score on last try: $8$ of $14$ pts$.$ See Details for more.

You can retry this question below

Based on the graph of $f^{\text{'}}$ above, we would expect $f$ to be increasing on the interval $(-00,-2)(1,00),.$

Based on the graph of $f^{\text{'}}$ above, we would expect $f$ to be decreasing on the interval

Based on the graph of $f^{\text{'}}$ above, we would expect $f$ to be concave up on the interval

Based on the graph of $f^{\text{'}}$ above, we would expect $f$ to be concave down on the interval

Based on the graph of $f^{\text{'}}$ we would expect the graph of $f$ to have a relative minimum at $x=$

Based on the graph of $f^{\text{'}}$ we would expect the graph of $f$ to have a relative maximum at $x=$

Based on the graph of $f^{\text{'}}$ we would expect the graph of $f$ to have an inflection point at $x=$

Enter your answer as a decimal.