Solve 7b and use excel sheet and table from another Q

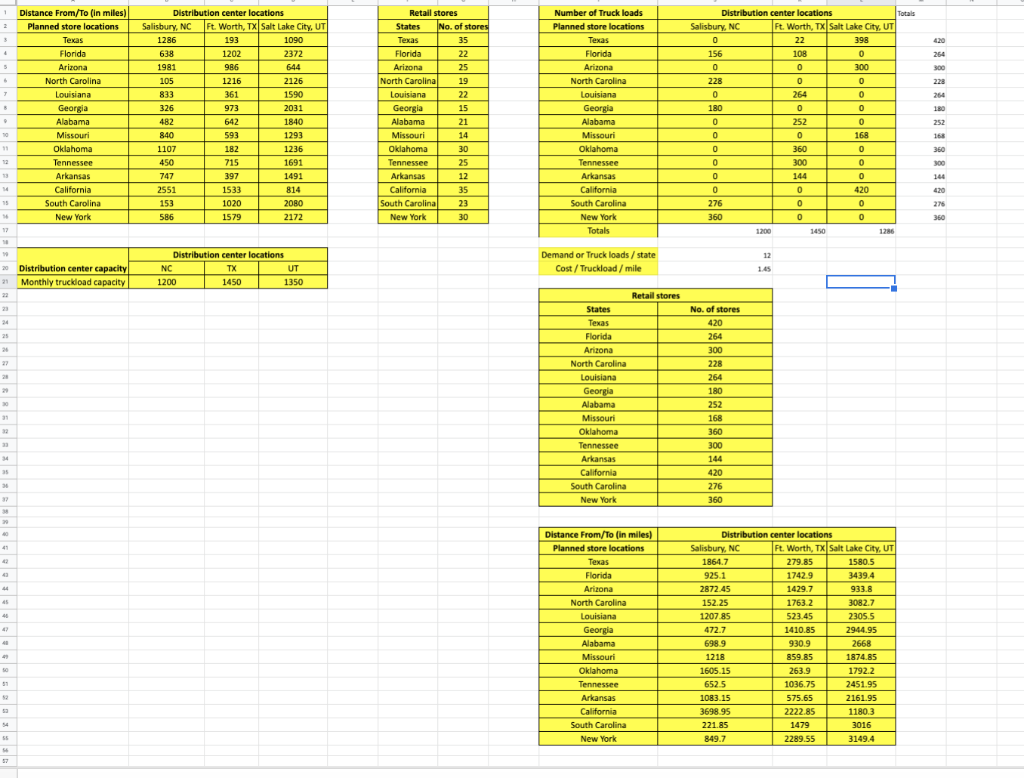
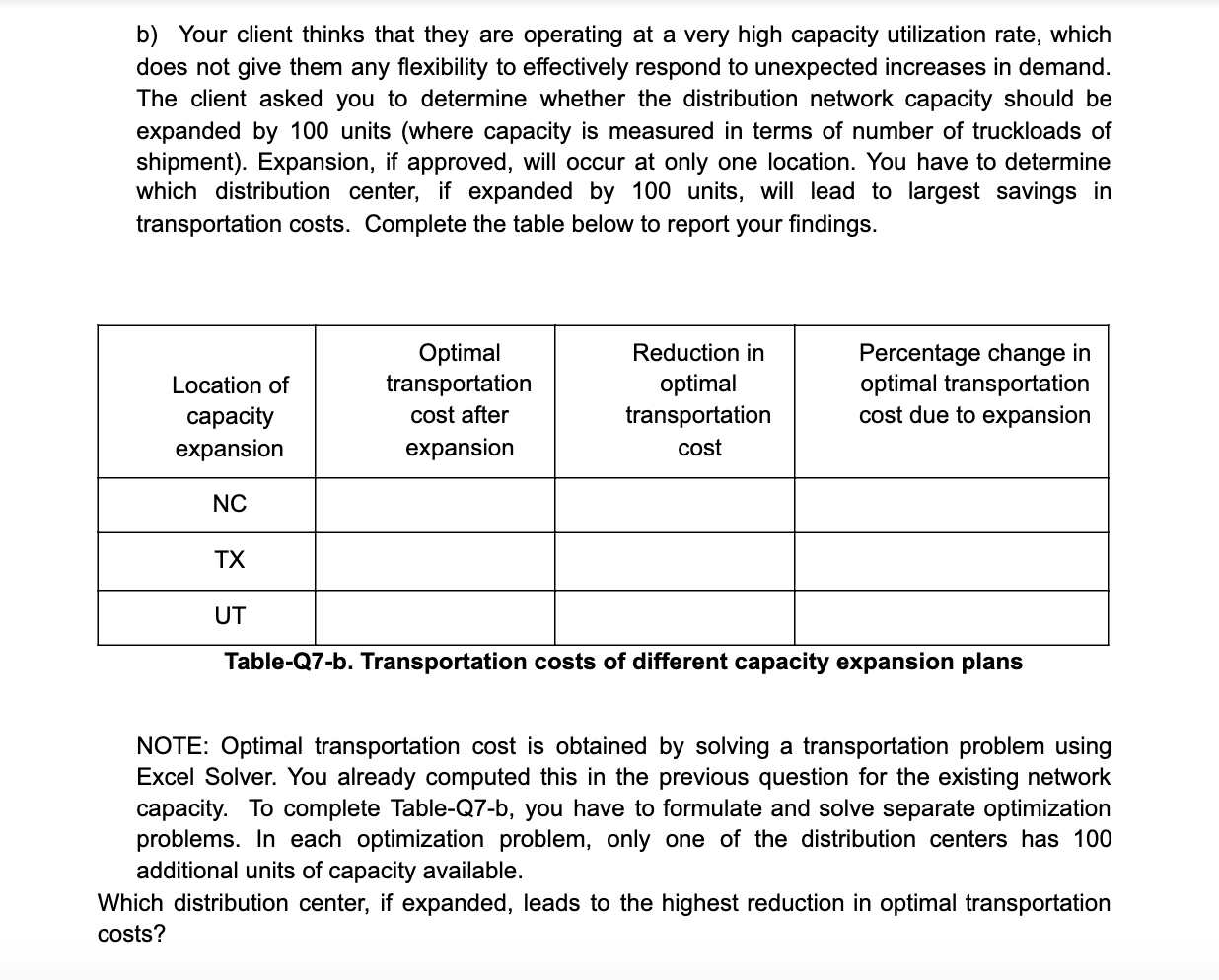
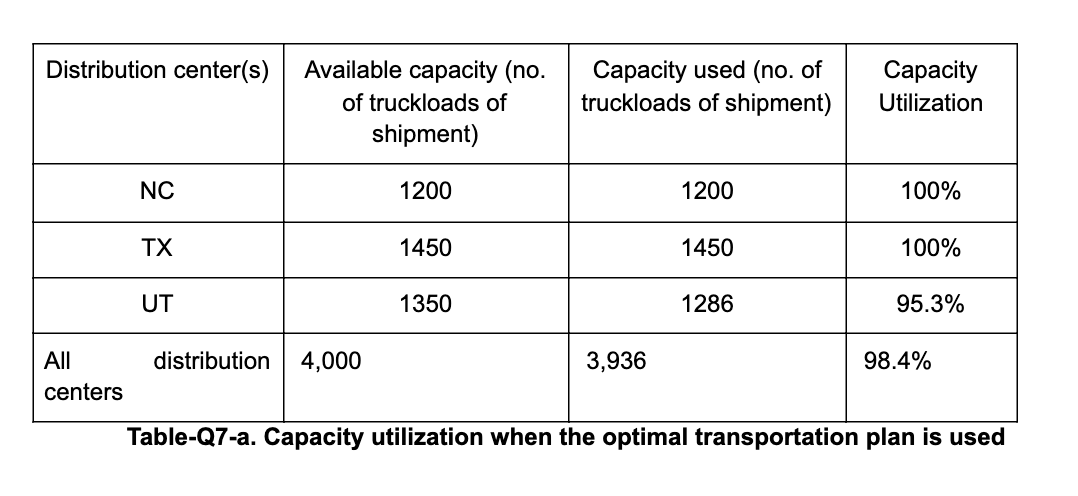
Totals 398 4 264 Distribution center locations Salisbury, NC Ft. Worth, TX Salt Lake City, UT 1286 193 1090 638 1202 2372 1981 986 644 105 1216 2126 833 361 1590 326 973 2031 482 642 1840 300 228 . 7 264 Distance From/to (in miles) Planned store locations Texas Florida Arizona North Carolina Louisiana Georgia Alabama Missouri Oklahoma Tennessee Arkansas California South Carolina New York 180 Retail stores States No. of stores Texas 35 Florida Arizona 25 North Carolina 19 Louisiana 22 Georgia 15 Alabama 21 Missouri 14 Oklahoma 30 Tennessee 25 Arkansas 12 California 35 South Carolina 23 New York 30 Number of Truck loads Planned store locations Texas Florida Arizona North Carolina Louisiana Georgia Alabama Missouri Oklahoma Tennessee Arkansas California South Carolina New York Totals Distribution center locations Salisbury, NC Ft. Worth, TX Salt Lake City, UT 0 22 156 108 O 0 0 300 228 0 0 0 264 0 180 0 0 0 252 0 0 0 168 0 360 0 0 300 0 0 0 144 0 0 0 420 276 0 0 360 0 0 1200 1450 1286 252 10 1293 168 840 1107 450 360 593 182 715 397 12 300 144 747 2551 153 586 1236 1691 1491 814 2080 2172 1533 1020 1579 276 360 17 12 Distribution center locations NC TX UT 1200 1450 1350 Demand or Truck loads/state Cost / Truckload/mile 20 Distribution center capacity 21 Monthly truckload capacity Retail stores 21 States Texas Florida Arizona North Carolina Louisiana Georgia Alabama Missouri Oklahoma Tennessee Arkansas California South Carolina New York No. of stores 420 264 300 228 264 180 252 31 168 360 300 144 420 276 360 30 41 Distance From/To (in miles) Planned store locations Texas Florida Arizona North Carolina Louisiana Georgia Alabama Missouri Oklahoma Tennessee Arkansas California South Carolina New York Distribution center locations Salisbury, NC Ft. Worth, TX Salt Lake City, UT 1864.7 279.85 1580.5 925.1 17420 3439.4 2872.45 1429.7 933.8 152.25 17632 3082.7 1207.85 523.45 2305 472.7 1410.85 2944.95 698.9 930.9 2668 1218 859.85 1874.85 1605.15 263.9 1792.2 652.5 1036.75 2451.95 1083.15 575.65 2161.95 3698.95 2222.85 11803 221.85 1479 3016 849.7 2289.55 3149.4 55 b) Your client thinks that they are operating at a very high capacity utilization rate, which does not give them any flexibility to effectively respond to unexpected increases in demand. The client asked you to determine whether the distribution network capacity should be expanded by 100 units (where capacity is measured in terms of number of truckloads of shipment). Expansion, if approved, will occur at only one location. You have to determine which distribution center, if expanded by 100 units, will lead to largest savings in transportation costs. Complete the table below to report your findings. Location of capacity expansion Optimal transportation cost after expansion Reduction in optimal transportation cost Percentage change in optimal transportation cost due to expansion NC TX UT Table-Q7-b. Transportation costs of different capacity expansion plans NOTE: Optimal transportation cost is obtained by solving a transportation problem using Excel Solver. You already computed this in the previous question for the existing network capacity. To complete Table-Q7-b, you have to formulate and solve separate optimization problems. In each optimization problem, only one of the distribution centers has 100 additional units of capacity available. Which distribution center, if expanded, leads to the highest reduction in optimal transportation costs? Distribution center(s) Available capacity (no. of truckloads of shipment) Capacity used (no. of truckloads of shipment) Capacity Utilization NC 1200 1200 100% TX 1450 1450 100% UT 1350 1286 95.3% distribution 4,000 3,936 98.4% All centers Table-Q7-a. Capacity utilization when the optimal transportation plan is used Totals 398 4 264 Distribution center locations Salisbury, NC Ft. Worth, TX Salt Lake City, UT 1286 193 1090 638 1202 2372 1981 986 644 105 1216 2126 833 361 1590 326 973 2031 482 642 1840 300 228 . 7 264 Distance From/to (in miles) Planned store locations Texas Florida Arizona North Carolina Louisiana Georgia Alabama Missouri Oklahoma Tennessee Arkansas California South Carolina New York 180 Retail stores States No. of stores Texas 35 Florida Arizona 25 North Carolina 19 Louisiana 22 Georgia 15 Alabama 21 Missouri 14 Oklahoma 30 Tennessee 25 Arkansas 12 California 35 South Carolina 23 New York 30 Number of Truck loads Planned store locations Texas Florida Arizona North Carolina Louisiana Georgia Alabama Missouri Oklahoma Tennessee Arkansas California South Carolina New York Totals Distribution center locations Salisbury, NC Ft. Worth, TX Salt Lake City, UT 0 22 156 108 O 0 0 300 228 0 0 0 264 0 180 0 0 0 252 0 0 0 168 0 360 0 0 300 0 0 0 144 0 0 0 420 276 0 0 360 0 0 1200 1450 1286 252 10 1293 168 840 1107 450 360 593 182 715 397 12 300 144 747 2551 153 586 1236 1691 1491 814 2080 2172 1533 1020 1579 276 360 17 12 Distribution center locations NC TX UT 1200 1450 1350 Demand or Truck loads/state Cost / Truckload/mile 20 Distribution center capacity 21 Monthly truckload capacity Retail stores 21 States Texas Florida Arizona North Carolina Louisiana Georgia Alabama Missouri Oklahoma Tennessee Arkansas California South Carolina New York No. of stores 420 264 300 228 264 180 252 31 168 360 300 144 420 276 360 30 41 Distance From/To (in miles) Planned store locations Texas Florida Arizona North Carolina Louisiana Georgia Alabama Missouri Oklahoma Tennessee Arkansas California South Carolina New York Distribution center locations Salisbury, NC Ft. Worth, TX Salt Lake City, UT 1864.7 279.85 1580.5 925.1 17420 3439.4 2872.45 1429.7 933.8 152.25 17632 3082.7 1207.85 523.45 2305 472.7 1410.85 2944.95 698.9 930.9 2668 1218 859.85 1874.85 1605.15 263.9 1792.2 652.5 1036.75 2451.95 1083.15 575.65 2161.95 3698.95 2222.85 11803 221.85 1479 3016 849.7 2289.55 3149.4 55 b) Your client thinks that they are operating at a very high capacity utilization rate, which does not give them any flexibility to effectively respond to unexpected increases in demand. The client asked you to determine whether the distribution network capacity should be expanded by 100 units (where capacity is measured in terms of number of truckloads of shipment). Expansion, if approved, will occur at only one location. You have to determine which distribution center, if expanded by 100 units, will lead to largest savings in transportation costs. Complete the table below to report your findings. Location of capacity expansion Optimal transportation cost after expansion Reduction in optimal transportation cost Percentage change in optimal transportation cost due to expansion NC TX UT Table-Q7-b. Transportation costs of different capacity expansion plans NOTE: Optimal transportation cost is obtained by solving a transportation problem using Excel Solver. You already computed this in the previous question for the existing network capacity. To complete Table-Q7-b, you have to formulate and solve separate optimization problems. In each optimization problem, only one of the distribution centers has 100 additional units of capacity available. Which distribution center, if expanded, leads to the highest reduction in optimal transportation costs? Distribution center(s) Available capacity (no. of truckloads of shipment) Capacity used (no. of truckloads of shipment) Capacity Utilization NC 1200 1200 100% TX 1450 1450 100% UT 1350 1286 95.3% distribution 4,000 3,936 98.4% All centers Table-Q7-a. Capacity utilization when the optimal transportation plan is used