Solve by matlab and submitte m-file

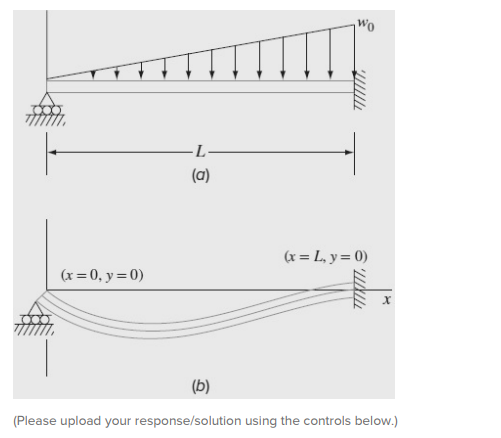
The figure given below shows a uniform beam subject to a linearly increasing distributed load. The equation for the resulting elastic curve is as follows: EI (1x = 7) = 0 Note that the analytical solution for the resulting elastic curve is as follows: 120EIL (-38 + 2Lr8 L*x) Use bvp4c to plot the result for the differential equation for the elastic curve for L = 600 cm, E = 50,000 kN/cm2, 1 = 30,000 cm4, and wo = 2.5 kN/cm and compare with the analytical solution. y = Wo TTTTTTTT L (a) (x = L, y = 0) (x=0, y=0) TI X (b) (Please upload your response/solution using the controls below.) The figure given below shows a uniform beam subject to a linearly increasing distributed load. The equation for the resulting elastic curve is as follows: EI (1x = 7) = 0 Note that the analytical solution for the resulting elastic curve is as follows: 120EIL (-38 + 2Lr8 L*x) Use bvp4c to plot the result for the differential equation for the elastic curve for L = 600 cm, E = 50,000 kN/cm2, 1 = 30,000 cm4, and wo = 2.5 kN/cm and compare with the analytical solution. y = Wo TTTTTTTT L (a) (x = L, y = 0) (x=0, y=0) TI X (b) (Please upload your response/solution using the controls below.)