Question: Solve d y d x = y t a n x using separation of variables given the inital condition y ( 0 ) = 1
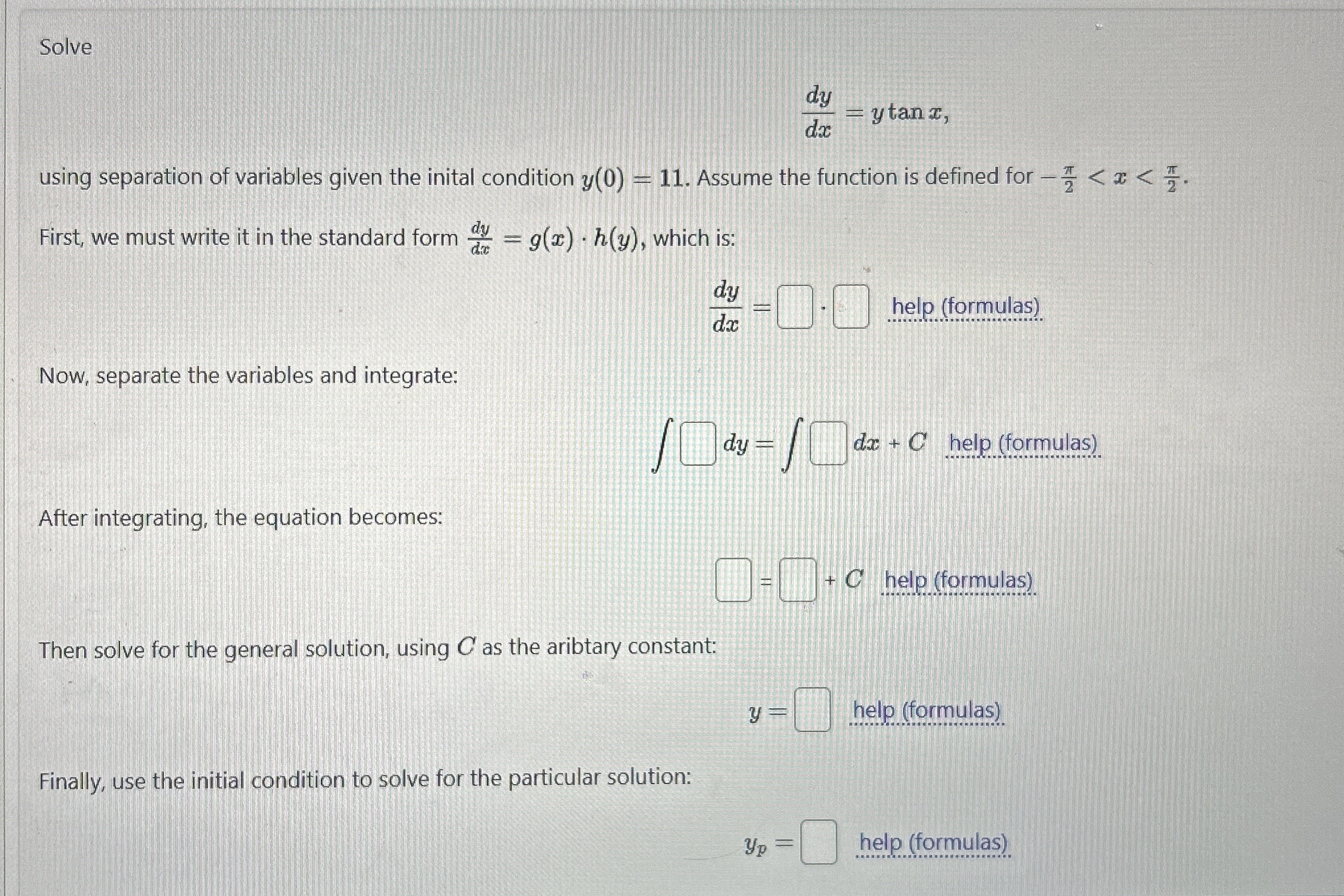
Solve
using separation of variables given the inital condition Assume the function is defined for help help help help
First, must write the standard form which :
help
Now, separate the variables and integrate:
help
After integrating, the equation becomes:
help
Then solve for the general solution, using the aribtary constant:
help
Finally, use the initial condition solve for the particular solution:
help
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


