Solve for graph 3 only.

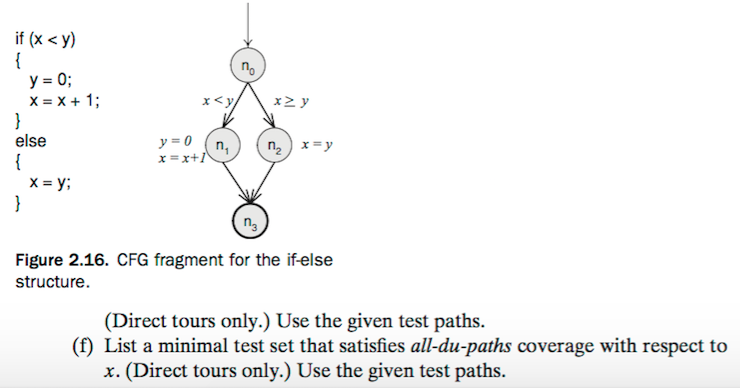
1. Below are four graphs, each of which is defined by the sets of nodes, initial nodes, final nodes, edges, and defs and uses. Each graph also contains a col- lection of test paths. Answer the following questions about each graph. Graph I. N={0, 1, 2, 3, 4, 5, 6, 7} E-{(0, 1), (1, 2), (1, 7), (2, 3), (2, 4), (3, 2), def(0) = def(3) = use(5) = use(7) = {x) Test Paths Graph II. N={1, 2, 3, 4, 5, 6} ={1} Ny = {6} E = {(1, 2), (2, 3), (2, 6), (3, 4), (3, 5), (4,5), (5, 2)) def(x) 1,3 use(x) 3,6)I/ Assume the use of x in 3 precedes the def Test Paths: | | 11 = [0, 1, 7] 12 = [0, 1, 2, 4, 6, 1,7] 13 = [0, 1, 2, 4, 5, 6, 1,7] 14 = [0, 1, 2, 3, 2, 4, 6, 1,7] 15 = [0, 1, 2, 3, 2, 3, 2, 4, 5, 6, 1,7] t6 = [0, 1, 2, 3, 2, 4, 6, 1, 2, 4, 5, 6, 1,7] 11 = [1, 2, 6] r2=[1, 2, 3, 4, 5, 2, 3, 5, 2,6] t3=[1, 2, 3, 5, 2, 3, 4, 5, 2.6] t4= [1, 2, 3, 5, 2, 6] Graph IV. N={1, 2, 3, 4, 5, 6} N; = {1} N-16 E= {(1,2), (2,3), (2,6), (3,4), (3,5), (4,5). Graph III. N={1, 2, 3, 4, 5,6) = {1} E= {(1,2), (2,3), (3,4), (3,5), (45), (5,2), (2,6)} | | def(x)= {1.4 use(x)- (3, 5, 6) def(x) 1, 5) use(x) = {5. 6} // Assume the use of x in 5 pre- cedes the def Test Paths: Test Paths h=[1, 2, 3, 5, 2, 6] 11 = [1, 2, 6] r2=[1, 2, 3, 4, 5, 2, 3, 5, 2, 6] t3=[1, 2, 3, 5, 2, 3, 4, 5,2,6] =[1, 2, 3, 4, 5, 2, 6]