Question: SOLVE IN PYTHON! f ( x ) = x ^ cos ( x ^ 2 ) , integral from 0 to 4 ( f (
SOLVE IN PYTHON!
fx xcosx integral from to fxdx
Recall the left endpoint rule example illustrated below:
~~
where and
Follow the steps below. Only parts c and d require
printed output in your submitted work.
a Define a Python function that accepts an ordered pair representing an interval as its input and returns the numerical result of applying the left endpoint rule to fx on that interval.
b Use the function you wrote in part a to define a new Python list that contains the results of applying the left endpoint rule to fx on each subinterval in Partition.
c Sum the list from part b to obtain an approximation for the area under fx on Print your output without rounding. The result should be if you have set up your approximation correctly.
d The true value of integral from to fxdx to decimal places is Use this value to print an estimate for the error actual approximation
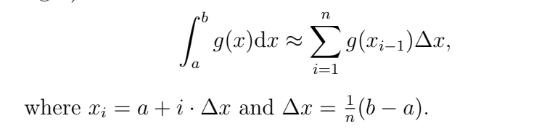
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


