Solve it for me please and select which option is correct

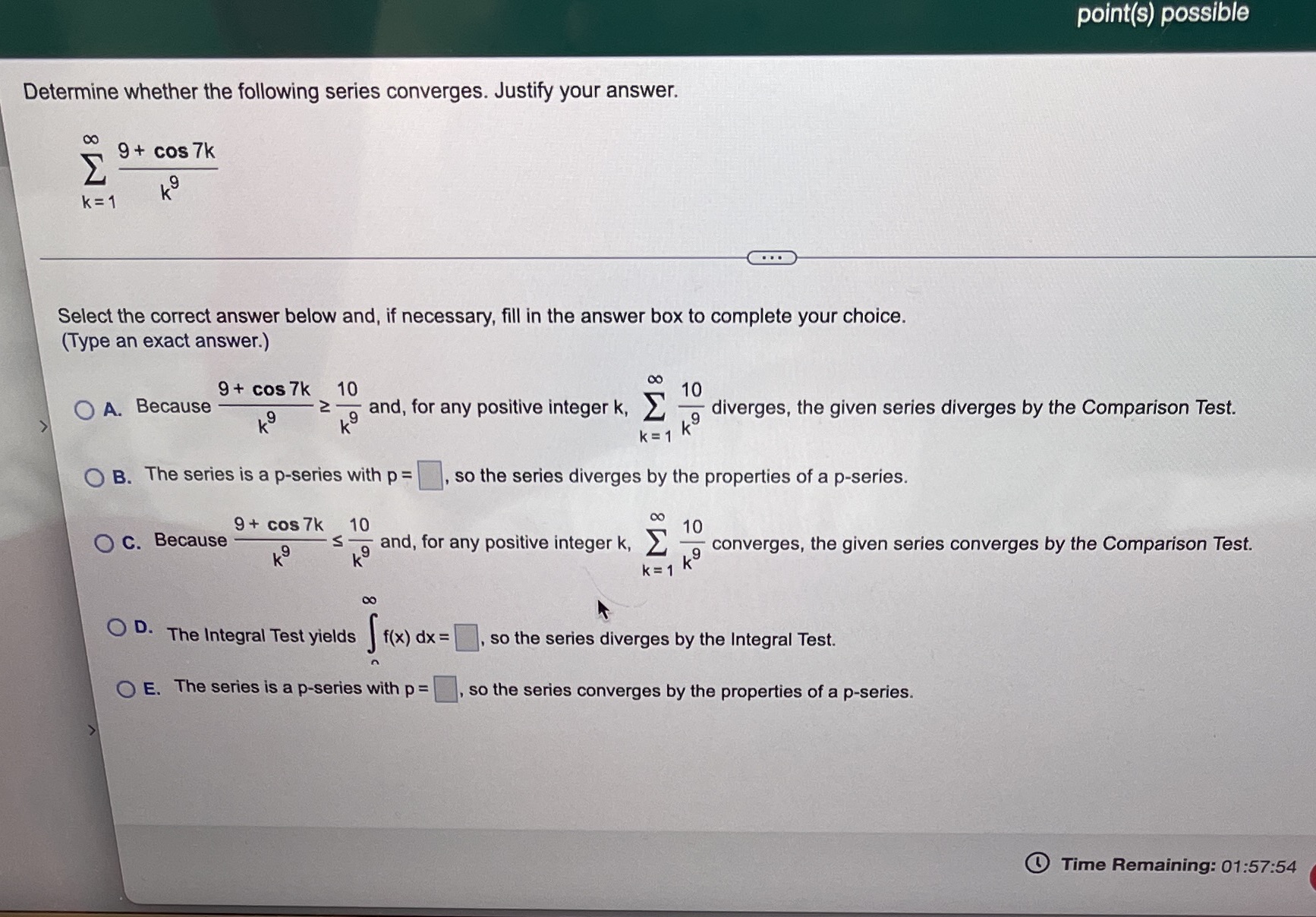
point(s) possible Determine whether the following series converges. Justify your answer. 9+ cos 7k M 8 K = 1 Select the correct answer below and, if necessary, fill in the answer box to complete your choice. (Type an exact answer.) 9 + cos 7k 10 10 O A. Because 2 iM 8 K9 19 and, for any positive integer k, diverges, the given series diverges by the Comparison Test. K O B. The series is a p-series with p = , so the series diverges by the properties of a p-series. 9 + cos 7k 10 O C. Because S and, for any positive integer k, 10 iM 8 K9 19 converges, the given series converges by the Comparison Test. K 8 O D. The Integral Test yields f(x) dx = , so the series diverges by the Integral Test. O E. The series is a p-series with p = , so the series converges by the properties of a p-series. Time Remaining: 01:57:54