solve it in c++/java/python

add output screen shot also

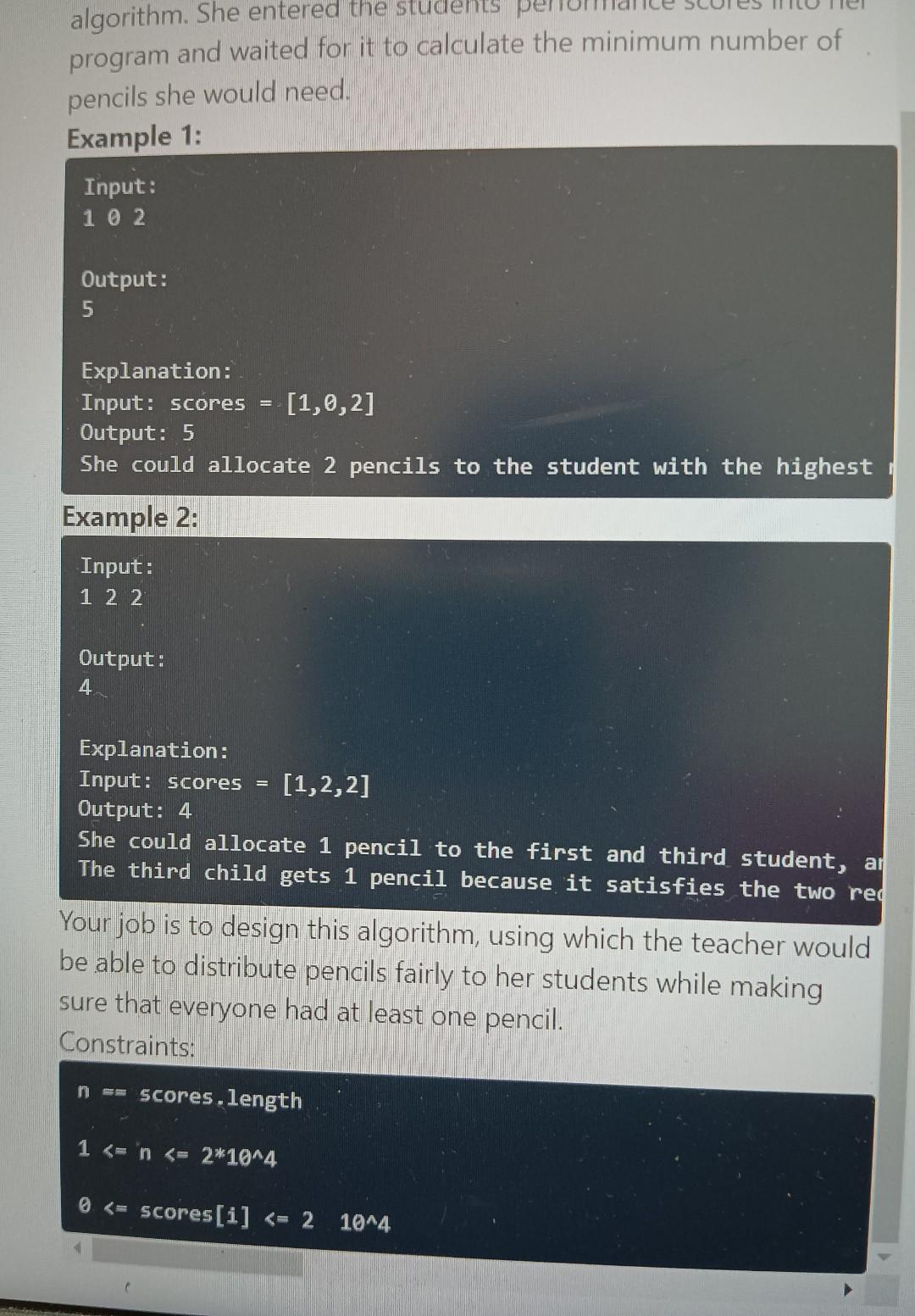
Once upon a time, there was a teacher who wanted to give pencils to her students based on their performance in class. She had a total of n students who were standing in a line. Each student was assigned a performance score value given in the integer array scores. The teacher had two requirements for distributing the pencils: 1. Each student must have at least one pencil. 2. Students with a higher score should get more pencils than their neighbours. The teacher was trying to figure out the minimum number of pencils she would need to distribute to the students. She wanted to make sure that she had enough pencils for everyone while also ensuring that the students with higher performance scores were appropriately rewarded. To help her figure this out, the teacher turned to her trusty algorithm. She entered the students' performance scores into her program and waited for it to calculate the minimurh number of pencils she would need. Example 1: Input: 102 Output: 5 Explanation: Input: scores =[1,0,2] Output: 5 She could allocate 2 pencils to the student with the highest program and waited for it to calculate the minimum number of pencils she would need. Example 1: Input: 102 Output: 5 Explanation: Input: scores =[1,0,2] 0utput: 5 She could allocate 2 pencils to the student with the highest Example 2: Input: 122 Output: 4 Explanation: Input: scores =[1,2,2] Output: 4 She could allocate 1 pencil to the first and third student, an The third child gets 1 pencil because it satisfies the two red Your job is to design this algorithm, using which the teacher would be able to distribute pencils fairly to her students while making sure that everyone had at least one pencil. Constraints: n=m cores. . length 1n2104 0=scores[i]