solve it with proper solution.

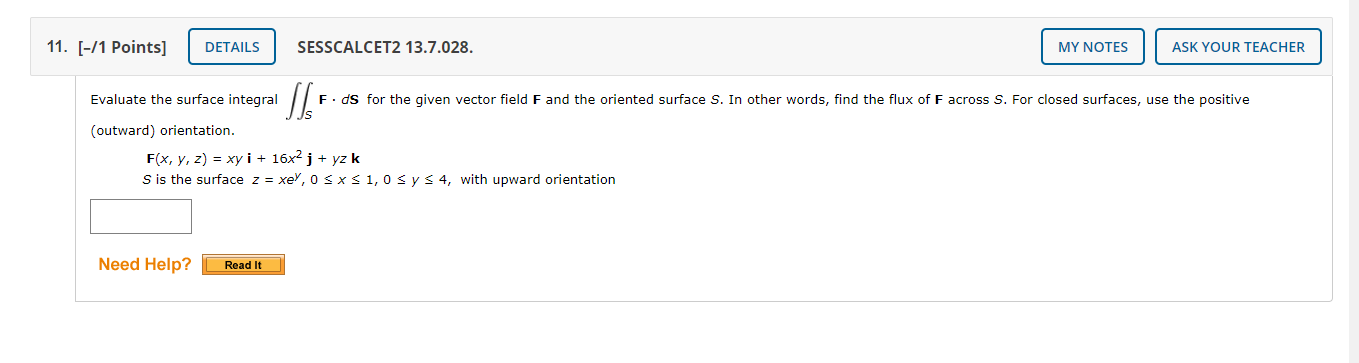
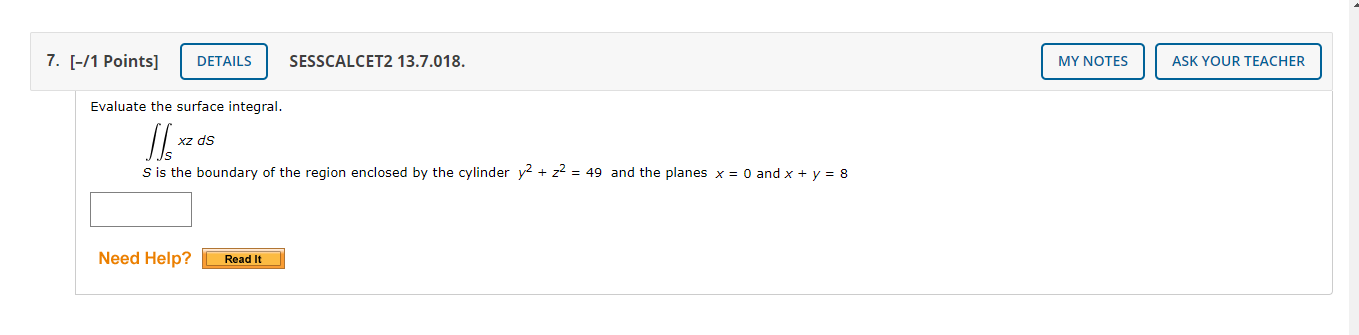
5. [-11 Points] SESSCALCETZ 133.013. Evaluate the surface integral. [322.15 5 is the part of the cone 22 = x2 + y2 that lies between the planes 2 = 4 and z = 5 ASK YOUR TEACHER Need Help? 11. [-/1 Points] DETAILS SESSCALCET2 13.7.028. MY NOTES ASK YOUR TEACHER Evaluate the surface integral F. ds for the given vector field F and the oriented surface S. In other words, find the flux of F across S, For closed surfaces, use the positive (outward) orientation. F(x, y, z) = xy i + 16x2 j + yz k S is the surface z = xey, 0 s x = 1, 0 sys 4, with upward orientation Need Help? Read ItEvaluate the surface integral. [Lads S is the boundary of the region enclosed by the cylinder 1.!2 + 22 = 49 and the planes x : U andx + y : B Need Help? W; TopicQ , Hull 2: (Parametric Sun x + 6 9 C i webassign.net/webjStudentg'AssignrnentaResponses/Iast?dep=246'i3343#Q6 The equation x4 + y2 = 72 describes a cylinder, and the intersection circle is above the xyiplane and on this cylinder. The z-value of points on this circle can be Found by solving 2 : \\f x2 + y2 and X2 + y2 = 72 simultaneously to nd 2, thereby obtaining z = 1,\" 72 m . I Part4of Since we want the portion of the sphere which is above this circle, we return to the parametric representation Z = \\f 144 \"2 y2 and iimitzto be at least \\/ 72. We, therefore, have \"1447!? 7v: :22 \"'7 . which means 1.:2 + v2 I J pg 72. Part50f An alternative approach involves using spherical coordinates (p, :9, (p). In spherical coordinates, the sphere has the equation 9 : I J p12 Therefore, we can use 9 and q) as parameters and use the equations that ailow us to convert from spherical to rectangular coordinates. We would then have x: 12sinqncos|9 y