Question: solve it with proper solution. VA Topic 9 - HW 2: (Parametric Surfa X + X > C A webassign.net/web/Student/Assignment-Responses/submit?dep=24613343&tags=autosave#question2146101_3 . . . 7. [-/1
solve it with proper solution.
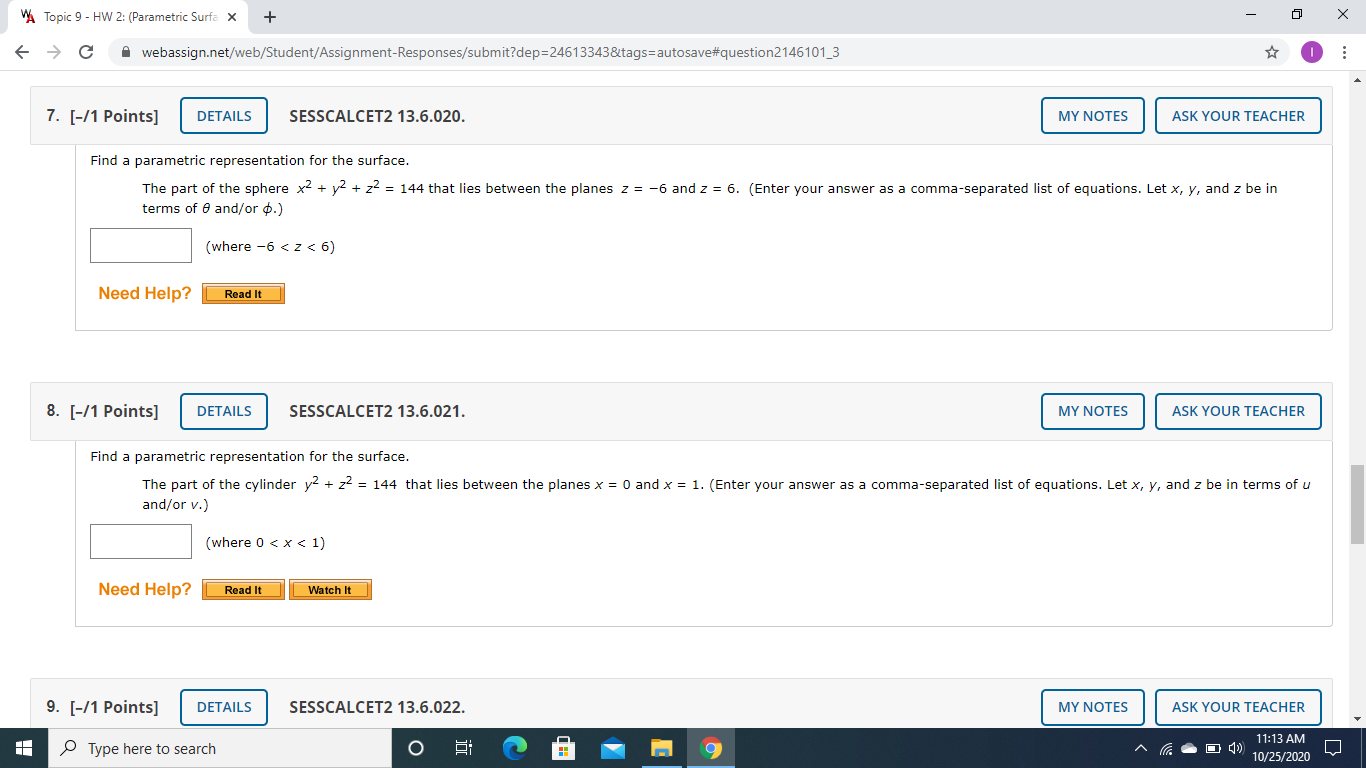
![[-/1 Points] DETAILS SESSCALCET2 13.6.020. MY NOTES ASK YOUR TEACHER Find a](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/671cda260d7b7_101671cda25d8276.jpg)
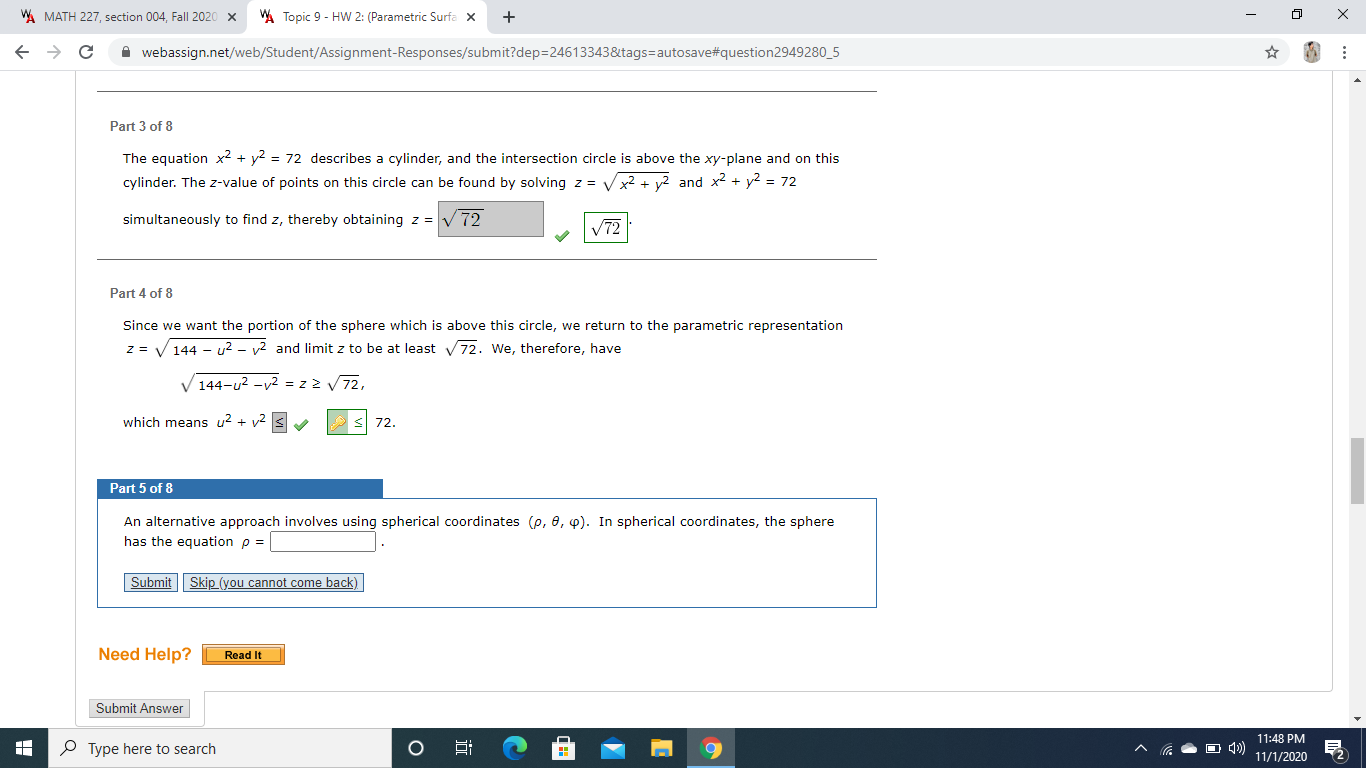
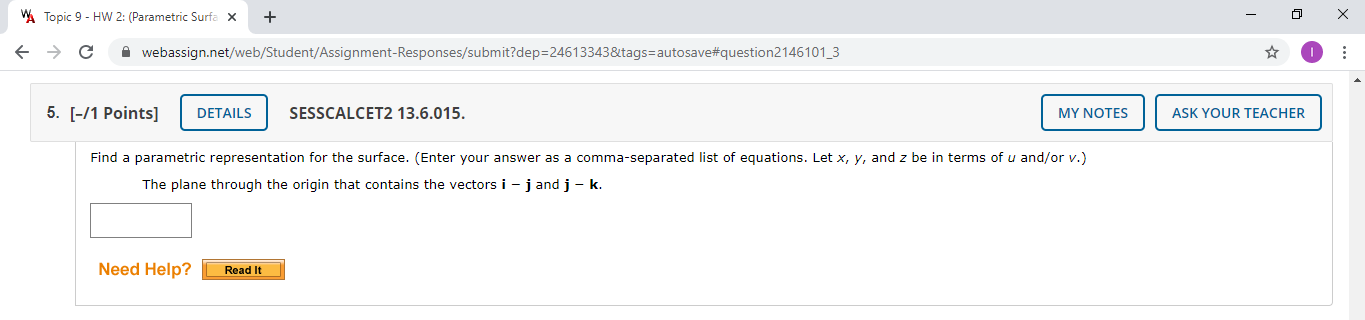
VA Topic 9 - HW 2: (Parametric Surfa X + X > C A webassign.net/web/Student/Assignment-Responses/submit?dep=24613343&tags=autosave#question2146101_3 . . . 7. [-/1 Points] DETAILS SESSCALCET2 13.6.020. MY NOTES ASK YOUR TEACHER Find a parametric representation for the surface. The part of the sphere x2 + yz + 2 C A webassign.net/web/Student/Assignment-Responses/submit?dep=24613343&tags=autosave#question2146101_3 . . . 5. [-/1 Points] DETAILS SESSCALCET2 13.6.015. MY NOTES ASK YOUR TEACHER Find a parametric representation for the surface. (Enter your answer as a comma-separated list of equations. Let x, y, and z be in terms of u and/or v.) The plane through the origin that contains the vectors i - j and j - k. Need Help? Read It12. [-/1 Points] DETAILS SESSCALCET2 13.6.038. MY NOTES ASK YOUR TEACHER Find the area of the surface. The part of the surface z = 5 + 5x + 2yz that lies above the triangle with vertices (0, 0), (0, 1), (2, 1). Need Help? Read It Type here to search 9 11:13 AM 10/25/2020VA MATH 227, section 004, Fall 2020 x VA Topic 9 - HW 2: (Parametric Surfa X + X - > C A webassign.net/web/Student/Assignment-Responses/submit?dep=24613343&tags=autosave#question2949280_5 Part 3 of 8 The equation x2 + yz = 72 describes a cylinder, and the intersection circle is above the xy-plane and on this cylinder. The z-value of points on this circle can be found by solving z = v x2 + y2 and x2 + yz = 72 simultaneously to find z, thereby obtaining z = v 72 V72 Part 4 of 8 Since we want the portion of the sphere which is above this circle, we return to the parametric representation z = \\ 144 - U2 - v2 and limit z to be at least v 72. We, therefore, have /144-12 -V2 = 2 2 \\72, which means u2 + 2 s 72. Part 5 of 8 An alternative approach involves using spherical coordinates (p, 0, 4). In spherical coordinates, the sphere has the equation p = Submit Skip (you cannot come back) Need Help? Read It Submit Answer Type here to search O 9 11:48 PM 11/1/2020
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


