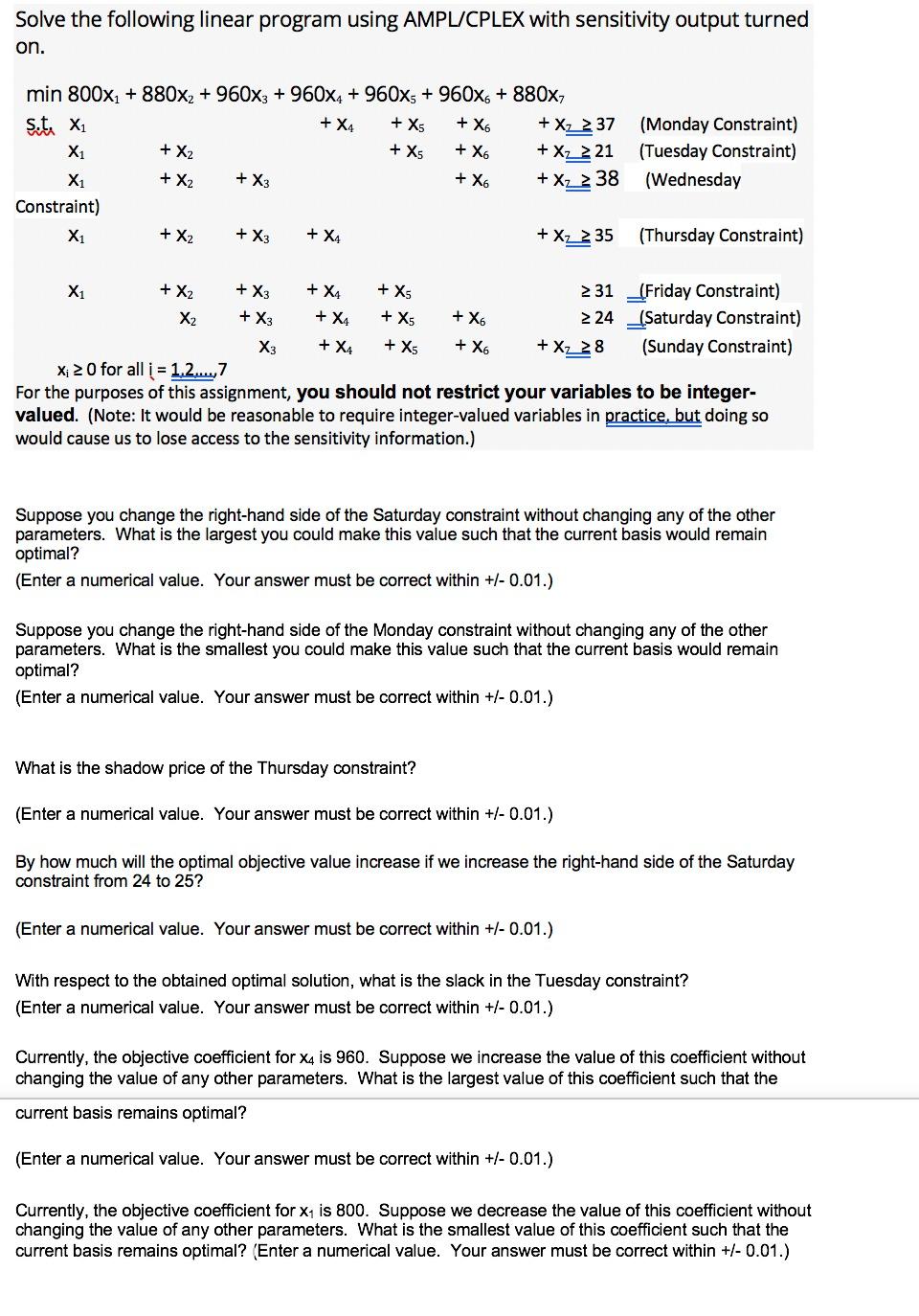
Question: Solve the following linear program using AMPL/CPLEX with sensitivity output turned on. + X5 min 800x: +880x2 + 960x3 + 960x4 + 960x5 + 960X+
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


