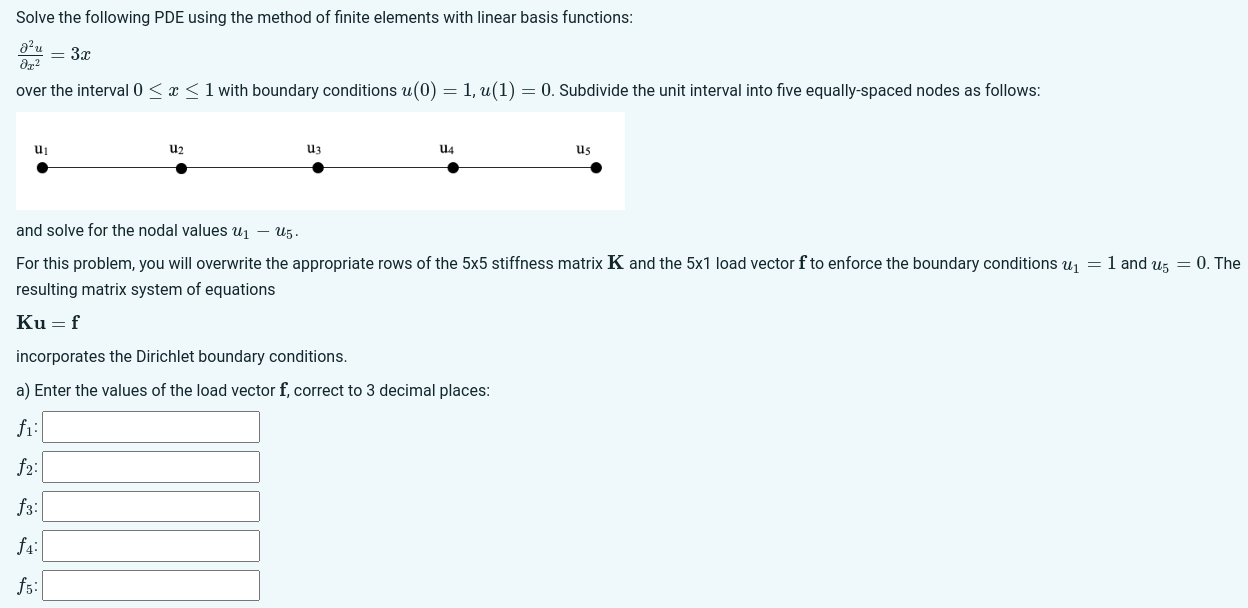
Solve the following PDE using the method of finite elements with linear basis functions: Ju 3x 2 over the interval 0 < x < 1 with boundary conditions u(0) = 1, u(1) = 0. Subdivide the unit interval into five equally-spaced nodes as follows: U2 U3 U4 us and solve for the nodal values u - U5. For this problem, you will overwrite the appropriate rows of the 5x5 stiffness matrix K and the 5x1 load vector f to enforce the boundary conditions u resulting matrix system of equations Ku = f incorporates the Dirichlet boundary conditions. a) Enter the values of the load vector f, correct to 3 decimal places: fi: f2: fa f4: fs: = 1 and us = 0. The