Solve the following questions

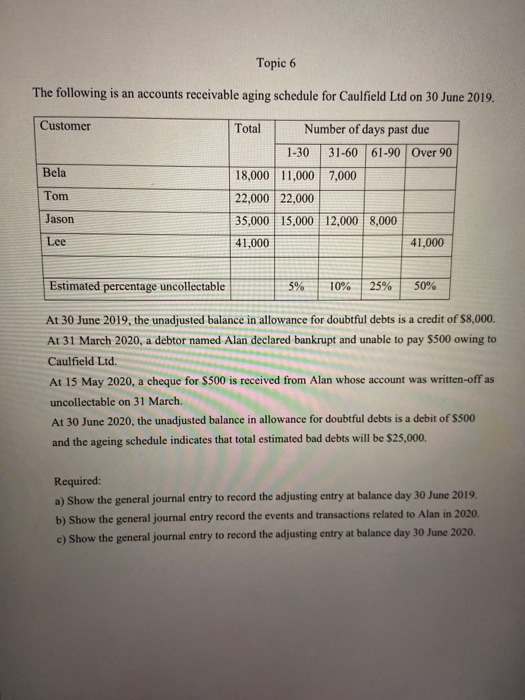
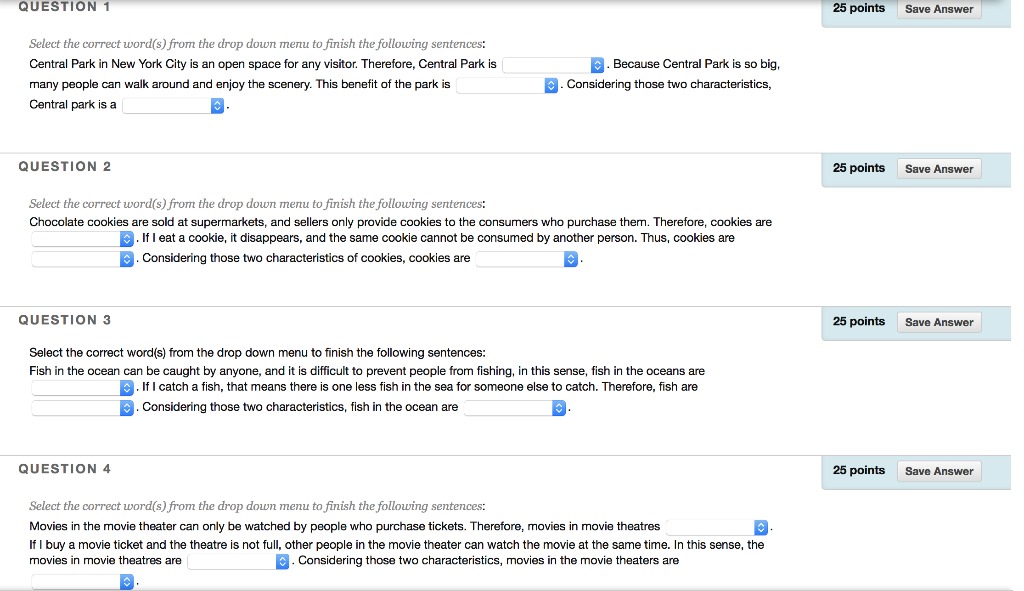
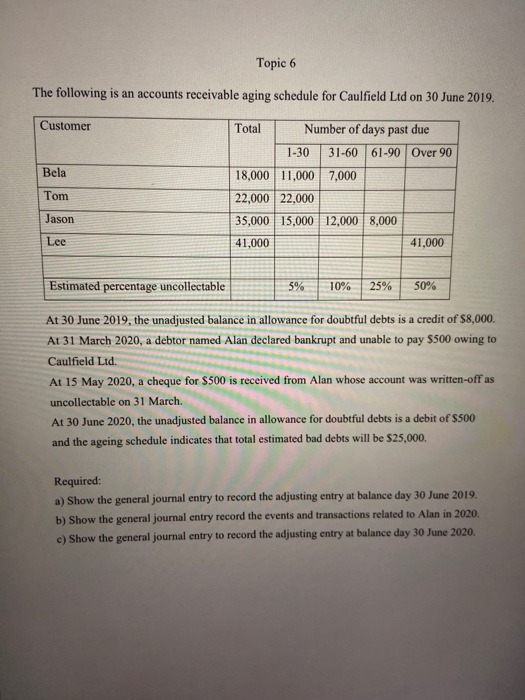
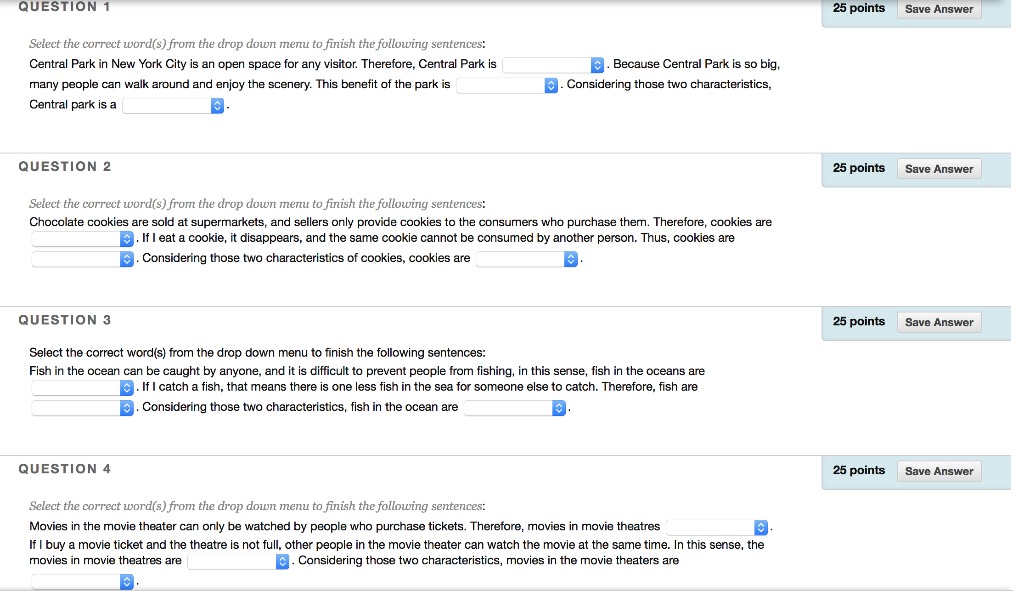
Simple linear regression is a statistical method that allows us to summarize and study relationships between two continuous (quantitative) variables: One variable, denoted X, is regarded as the predictor, explanatory, or independent variable. The other variable, denoted Y, is regarded as the response, outcome, or dependent variable. Suppose that we are given n-i.i.d observations { (x;, y;)}"_, from the assumed simple linear regression model Y = BIX + Bo + . Answer the following questions on simple linear regression. 5-a. Denote 1 and Bo as the point estimators of B, and Bo, respectively, that are obtained through the least squares method. Show, step by step, that the two point estimators are unbiased. Derive the least squares estimator of of and determine whether it is unbiased or not. Show your work step by step. 5-b. Calculate _'_1(yi - Bix; - Bo) (Bix, + Bo). Determine whether the point (X, Y) is on the line Y = 1X + Bo. Explain your reasoning mathematically. 5-c. Using the maximum likelihood estimation (MLE) technique, derive a point estimator for the coefficient B1 and the intercept Bo, respectively. Determine whether the point estimators that you obtained via MLE are unbiased or not. Justify your conclusion mathematically. 5-d. Calculate the variance of the four estimators from Questions 5-a and 5-c, respectively. Show your work step by step. 5-e. Suppose that we are using the simple linear regression model Y = B1 X + Bo + 1 while the true model is Y = 1X1 + B2X2 + Bo + 82 where Bo, B1, and B2 are constants. We assume that the distributions of &, and e2 are both N(0,02), i.e., normal distribution with variance o?. We further assume that the two noise variables are uncorrelated. Find the least squares estimator of B, in this case and determine whether the point estimator that you obtain is biased or not. If it is biased, calculate the bias.Topic 6 The following is an accounts receivable aging schedule for Caulfield Lid on 30 June 2019. Customer Total Number of days past due 1-30 31-60 61-90 Over 90 Bela 18,000 11,000 7,000 Tom 22,000 22,000 Jason 35,000 15,000 12,000 8,000 Lee 41,000 41,000 Estimated percentage uncollectable 5% 10% 25% 50% At 30 June 2019, the unadjusted balance in allowance for doubtful debts is a credit of $8,000. At 31 March 2020, a debtor named Alan declared bankrupt and unable to pay $500 owing to Caulfield Lid. At 15 May 2020, a cheque for $500 is received from Alan whose account was written-off as uncollectable on 31 March. At 30 June 2020, the unadjusted balance in allowance for doubtful debts is a debit of $500 and the ageing schedule indicates that total estimated bad debts will be $25,000. Required: a) Show the general journal entry to record the adjusting entry at balance day 30 June 2019. b) Show the general journal entry record the events and transactions related to Alan in 2020. c) Show the general journal entry to record the adjusting entry at balance day 30 June 2020.QUESTION 1 25 points Save Answer Select the correct word(s) from the drop down menu to finish the following sentences: Central Park in New York City is an open space for any visitor. Therefore, Central Park is . Because Central Park is so big, many people can walk around and enjoy the scenery. This benefit of the park is . Considering those two characteristics, Central park is a QUESTION 2 25 points Save Answer Select the correct word(s) from the drop down menu to finish the following sentences: Chocolate cookies are sold at supermarkets, and sellers only provide cookies to the consumers who purchase them. Therefore, cookies are . If I eat a cookie, it disappears, and the same cookie cannot be consumed by another person. Thus, cookies are C. Considering those two characteristics of cookies, cookies are QUESTION 3 25 points Save Answer Select the correct word(s) from the drop down menu to finish the following sentences: Fish in the ocean can be caught by anyone, and it is difficult to prevent people from fishing, in this sense, fish in the oceans are C. If I catch a fish, that means there is one less fish in the sea for someone else to catch. Therefore, fish are . Considering those two characteristics, fish in the ocean are QUESTION 4 25 points Save Answer Select the correct word(s) from the drop down menu to finish the following sentences: Movies in the movie theater can only be watched by people who purchase tickets. Therefore, movies in movie theatres If I buy a movie ticket and the theatre is not full, other people in the movie theater can watch the movie at the same time. In this sense, the movies in movie theatres are C. Considering those two characteristics, movies in the movie theaters are1. (15 points) For the exercises below, transform the regression equation Yi = 60 +81Xli +$2X2i +pi so that you can use a t-statistic to test for the following restrictions. Show all your steps for full credit. a. (5 points) B1 = 1262 b. (5 points) B1 - 82 = 2 a) If we assume normality of u, then we know the exact distribution of B1, a t student b) If we do not assume normality of u but n is large, then we approximate the sampling distribution 3 2. (15 points) Consider the following model to explain CEO salaries in terms of various factors: salary = 30 + Blsales + $2mktval + 83ceoten + u, where: salary = 1990 compensation, $1000s; sales = 1990 firm sales, millions; mktval = market value, end 1990, mills; ceoten = years as ceo with company Next you perform the following regression: * R2 = 0.2013, SER = 529.67 a) (5 pts) What does each estimated coefficient on the individual variables (and constant term) mean quantitatively (do not worry about standard errors, as they are not given, or the measures of fit)? b) (5 pts) What is the forecasted salary of a CEO working in a firm with sales equal to 5,000 millions, market value equal to 10,000 millions, and 10 years of tenure? c) (5 pts) Eliminating the variable sales from your regression, the estimation regression becomes:" salary = 613.436 + .019sales + .023mktval + 12.703ceoten + u salary = 641.059 + .0369mktval + 11.525ceoten + u R2 = 0.184, SER = 533.58 Why do you think that the effect of mktval has changed now over part b. (very briefly describe)?(a) First consider an economy where the government budget is required to be balanced in recession. The economy is given by: Czcu+c1(YT) T=t+t1Y I=I_ G=T With{61{1,{t1{1 i. Derive an expression for Equilibrium output. ii. Suppose for that for some reason demand were to fall, so that en were to decrease. We are interested in by how much output would fall due to this decline in ca. Derive an expression for the decrease in y do to a decrease in Ca. (b) Now ippose that the economy is the same as above except that G = G, La. that G is constant, and the government budget is not required to be balanced in recession. i. Derive an expression for equilibrium output. ii. Derive an expression for the decrease in 3,; due to a decrease in [30. (c) Interpretation: i. Based on the expressions you derived in aii and bii, would the same decline in g cause a larger decline in the economy with a balanced budget requirement, or the economy in which the government was not required to run a balanced budget? ii. In economy a, the govermnent's budget remains balanced after the decline in output, i.e. that (T G) = 0. Suppose that in economy I: the government's budget was balanced before the decline in output. What happens to the government's budget after the decline in gutput; is it still balanced, in surplus, or decrt? 1.e (T G) 2: [1? iii. How do you think the condition of the government's budget af fects how the economy responds to a decline in demand in the two eoonomies above? How does the answer to part cii concern- ing the state of the government's budget relate to your answer in part ci concerning which economy would experience a. larger decline in output given the same fall in ca