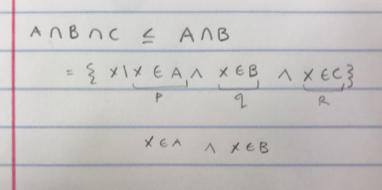
solve using identities

4 5 1\ 3 LOGICAL IDENTITIES PAP idempotence of P=PVP idempotence of PVQ=QVP conttativity of PAQE QAP commutativity of A (PVQIVR=PV (VR) associativity of v (PAQAR= PAQAR) associativity of A -(PVQ) =-PA-Q DeMorgan's Law -(PA) E-PV-Q PAQVR) = (PAQV(PAR) distributivity of over PVQAR) = (PVQ) A(PVR) distributivity of over PVT=T domination laws F= F. PATEP identity laws PVF =P PV-PT negation law PA-P=F --P) =P double negation law PV(PA) =P absorption laws PAPVQ) =P P Q = PVQ implication P Q -Q - -P contrapositive P-Q (P-QAQ - P) equivalente PAQ) -- R = P - Q - R esportation TABLE 1 Set Identities. Identity Vame Identity laws AU =A AU=A Domination laws AUU=U Anb=0 Idempotent laws AUA= A AnA = A (A) = A Complementation law Commutative laws AUB=BUA AB=BNA Associative laws AU (BUC) = (AUB)UC An(BNO)=(ANB) nC AN(BUC)=(ANB) U (ANC) AU(BOC)= (AUB)(AUC) Distributive laws De Morgan's laws AUB= AB AB=AUB Absorption laws AUAAB) = A A (AUB) = A AU=1 Ano Complement laws