Solve using Matlab. Gauss.m is attached below.

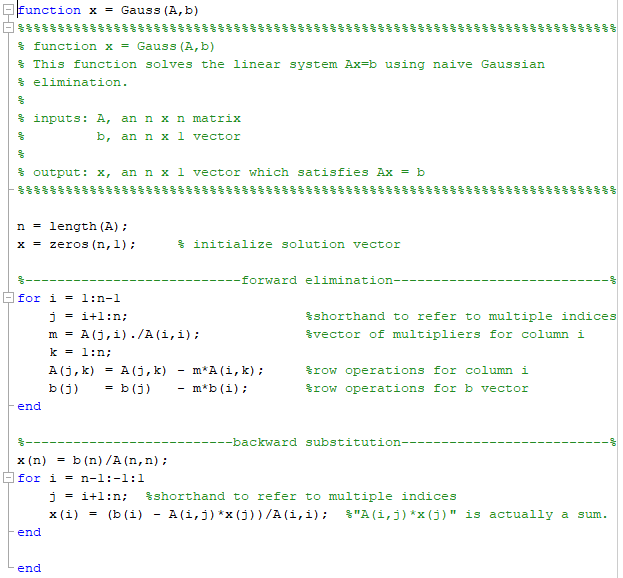
(3) An important aspect of constructing numerical solutions of linear systems, is the operation count. For example, in order to solve an n n system of linear equations via Gaussian elimination, the required niimber of multiplications, divisions and additions/subtractions (floating point operations, or flops) is -As n becomes large, we say the operation count is dominated by the largest quantity, i.e. that the operation count is O (n3). Verify this numerically as follows: (a) In a for loop, construct a random matrix A of size n n, and a random vector b of size n x 1, for n 100, 200,,1,000. (Use the commands A rand(n,n); and b randn,1):) (b) Inside the loop, use tic and toc to store the time it takes to solve Ax -b using Gauss.m. (c) On a log-log plot, display the times as a function of n. On the same plot, display the polynomial f(n) n. If the lines are parallel, then the operation count is confirmed. (d) Repeat this procedure, now using the built-in Matlab function ref. How does the operation count scale with n? That is, determine the value of p for which the time is (n)