Solve using Texas instrument BA II Plus

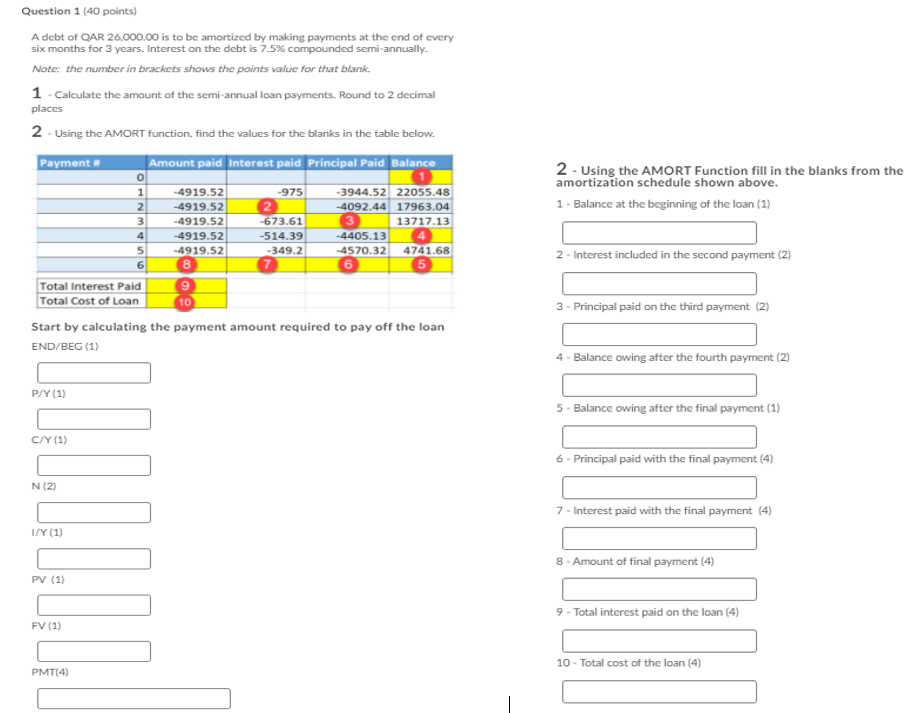
Question 1 (40 points) A debt of QAR 26,000.00 is to be amortized by making payments at the end of every six months for 3 years. Interest on the debt is 7.5% compounded semi-annually. Note: the number in brackets shows the points value for that blank. 1 - Calculate the amount of the semi-annual loan payments. Round to 2 decimal places 2 - Using the AMORT function, find the values for the blanks in the table below. Payment Amount paid Interest paid Principal Paid Balance -4919.52 -3944.52 22055.48 2 -4092.44 17963.04 -975 2 - Using the AMORT Function fill in the blanks from the amortization schedule shown above. 1 - Balance at the beginning of the loan (1) o 1 2 3 4 5 6 13717.13 -4919.52 -4919.52 -4919.52 -4919.52 8 -673.61 -514.39 -349.2 7 -4405.13 -4570.32 6 4741.68 2 - Interest included in the second payment (2) 3 - Principal paid on the third payment (2) Total Interest Paid 9 Total Cost of Loan 10 Start by calculating the payment amount required to pay off the loan END/BEG (1) 4 - Balance owing after the fourth payment (2) P/Y (1) 5. Balance owing after the final payment (1) C/Y (1) 6 - Principal paid with the final payment (4) N (2) 7 - Interest paid with the final payment (4) I/Y (1) 8 - Amount of final payment (4) PV (1) 9 - Total interest paid on the loan (4) FV (1) 10 - Total cost of the loan (4) PMT(4) Question 1 (40 points) A debt of QAR 26,000.00 is to be amortized by making payments at the end of every six months for 3 years. Interest on the debt is 7.5% compounded semi-annually. Note: the number in brackets shows the points value for that blank. 1 - Calculate the amount of the semi-annual loan payments. Round to 2 decimal places 2 - Using the AMORT function, find the values for the blanks in the table below. Payment Amount paid Interest paid Principal Paid Balance -4919.52 -3944.52 22055.48 2 -4092.44 17963.04 -975 2 - Using the AMORT Function fill in the blanks from the amortization schedule shown above. 1 - Balance at the beginning of the loan (1) o 1 2 3 4 5 6 13717.13 -4919.52 -4919.52 -4919.52 -4919.52 8 -673.61 -514.39 -349.2 7 -4405.13 -4570.32 6 4741.68 2 - Interest included in the second payment (2) 3 - Principal paid on the third payment (2) Total Interest Paid 9 Total Cost of Loan 10 Start by calculating the payment amount required to pay off the loan END/BEG (1) 4 - Balance owing after the fourth payment (2) P/Y (1) 5. Balance owing after the final payment (1) C/Y (1) 6 - Principal paid with the final payment (4) N (2) 7 - Interest paid with the final payment (4) I/Y (1) 8 - Amount of final payment (4) PV (1) 9 - Total interest paid on the loan (4) FV (1) 10 - Total cost of the loan (4) PMT(4)