SOLVE WITH MATLAB

PLEASE COMPLETE THE CODE ACCORDING TO THE PROBLEM

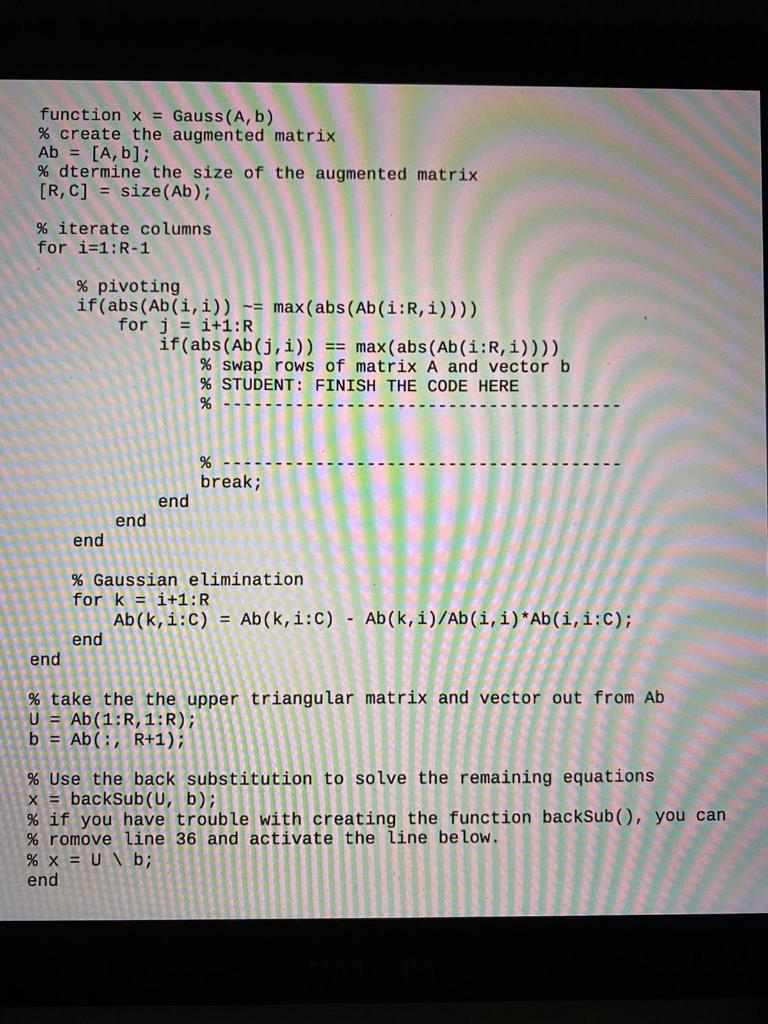
Problem) The truss shown below is composed of five elements and four nodes as shown. A vertical load P is applied at node 4. Bar elements land 2 have axial stiffnesses of 2AE, and bars 3, 4, and 5 have axial stiffness of AE. Here, A and E represent the cross-sectional area and modulus of elasticity of a bar and we have: E = 200 GPa, A= 8e-3 m , L = 2 m, P= 20 kN The structure has 3 unknowns, which are the displacements at the 3 joints (dzy, dzy, and day). The stiffness matrix of the structure (K) multiplied by the unknown displacement vector (X) gives us the vector of external forces (F). To obtain the unknown displacements at joints, we want to solve the system of equations K X=F: 459 TIT 45 EA K= L 1 0 -0.5 0 1 -0.5 -0.51 -0.5 1 [day] X = |dzy, F = [day] 0 1-P c) Modify the function Gauss.m that you completed such that it decomposes a given matrix into lower (L) and upper (U) triangular matrices (LU decomposition) using the Gauss elimination procedure and returns L and U. Subsequently, use the function to decompose matrix K into lower (L) and upper triangular (U) matrices. Does multiplying L and U give K? function x = Gauss (A,b) % create the augmented matrix Ab = [A,b]; % dtermine the size of the augmented matrix [R,C] = size(Ab); % iterate columns for i=1:R-1 % pivoting if(abs(Ab(i, i)) -= max(abs(Ab(i:R, i)))) for j = i+1:R if(abs(Ab(j,i)) == max(abs(Ab(i:R, i)))) % swap rows of matrix A and vector b % STUDENT: FINISH THE CODE HERE % % break; end end end % Gaussian elimination for k = i+1:R Ab(k,i:C) = Ab(k,i:c) - Ab(k, i)/Ab(i, i)*Ab(i,i:c); end end % take the the upper triangular matrix and vector out from Ab U = Ab(1:R, 1:R); b = Ab(:, R+1); % Use the back substitution to solve the remaining equations x = backSub(U, b) % if you have trouble with creating the function backSubo, you can % romove line 36 and activate the line below. % X = Ub; end Problem) The truss shown below is composed of five elements and four nodes as shown. A vertical load P is applied at node 4. Bar elements land 2 have axial stiffnesses of 2AE, and bars 3, 4, and 5 have axial stiffness of AE. Here, A and E represent the cross-sectional area and modulus of elasticity of a bar and we have: E = 200 GPa, A= 8e-3 m , L = 2 m, P= 20 kN The structure has 3 unknowns, which are the displacements at the 3 joints (dzy, dzy, and day). The stiffness matrix of the structure (K) multiplied by the unknown displacement vector (X) gives us the vector of external forces (F). To obtain the unknown displacements at joints, we want to solve the system of equations K X=F: 459 TIT 45 EA K= L 1 0 -0.5 0 1 -0.5 -0.51 -0.5 1 [day] X = |dzy, F = [day] 0 1-P c) Modify the function Gauss.m that you completed such that it decomposes a given matrix into lower (L) and upper (U) triangular matrices (LU decomposition) using the Gauss elimination procedure and returns L and U. Subsequently, use the function to decompose matrix K into lower (L) and upper triangular (U) matrices. Does multiplying L and U give K? function x = Gauss (A,b) % create the augmented matrix Ab = [A,b]; % dtermine the size of the augmented matrix [R,C] = size(Ab); % iterate columns for i=1:R-1 % pivoting if(abs(Ab(i, i)) -= max(abs(Ab(i:R, i)))) for j = i+1:R if(abs(Ab(j,i)) == max(abs(Ab(i:R, i)))) % swap rows of matrix A and vector b % STUDENT: FINISH THE CODE HERE % % break; end end end % Gaussian elimination for k = i+1:R Ab(k,i:C) = Ab(k,i:c) - Ab(k, i)/Ab(i, i)*Ab(i,i:c); end end % take the the upper triangular matrix and vector out from Ab U = Ab(1:R, 1:R); b = Ab(:, R+1); % Use the back substitution to solve the remaining equations x = backSub(U, b) % if you have trouble with creating the function backSubo, you can % romove line 36 and activate the line below. % X = Ub; end