Solving Some Physics Problems.

At this point we could implement floating point math. Our computer does have sufficient instructions, but I think our energy would be better served by solving some

physics problems with our simple computer.

You are standing on top of a $100-m$ tower and release a $10-kg$ ball. We want to simulate the ball being released and hitting the ground. Write a code to solve this problem

using the Euler method.

You must consider the following

how to best scale the problem to minimize round off errors

choosing the integration time$-$step to minimize trunction errors

To answer these points introduce LENGTH$\_$SCALE and TIME$\_$SCALE factors that will adjust your inputs, thus your code should adopt an initialization block as listed

below. You may need to take your answer returned from the virtual computer and scale it back to MKS using TIME$\_$SCALE $($see below for an example$).$ The idea is to

scale the physics problem to fit in our force numerical scale. This is necessary to solve most modern physics problems even with full $64-$bit floating$-$point operations.

You make include the while$($var$)$ or while$($not var$)$ command in your code to aid with boundary detection. Thus, you cannot use while$(x>y)$ or other

variations. It may help to note that True $==1$ and False $==0.$ Thus you are creating a map from your physical space to the simulation space.

Answer the following questions.

How long does it take for the ball to reach the ground using your simulation? We will call this the drop$-$time $.$

Calculate the analytic solution and compare to your answer. How well do they match?

Plot a map of drop$-$time as a function of TIME$\_$SCALE and LENGTH$\_$SCALE. To visualize the results use MatPlotlib pcolormesh or imshow that has TIME$\_$SCALE

on the $x-$axis and LENGTH$\_$SCALE on the y$-$axis. To create your map you can wrap your drop$-$time code calculator into any python construct to gather results.

Discuss your map in the content of truncation and round$-$off error.

What values of TIME$\_$SCALE and LENGTH$\_$SCALE produce the best results $($precison relative to known answer$)?$

What are the maximum and minimum useable values of TIME$\_$SCALE and LENGTH$\_$SCALE?

What valeus of TIME$\_$SCALE and LENGTH$\_$SCALE optimize the compute time $($e$.$g$.,$ minimize prg$\_$cnt$)$ and precision?

Hint #$1$: I needed to use a grid of $100100$ to properly explore the behaviour of changing scales. Calculating large grids may take $10-30$ minutes depending on your setup.

Consider using the tqdm package to monitor the run$-$time of your codes.

Hint #$2$: Note, you may encounter solutions that do not converge and give pure numerical noise, thus you should take care when selecting your colourmap range with

imshow or pcolormesh.

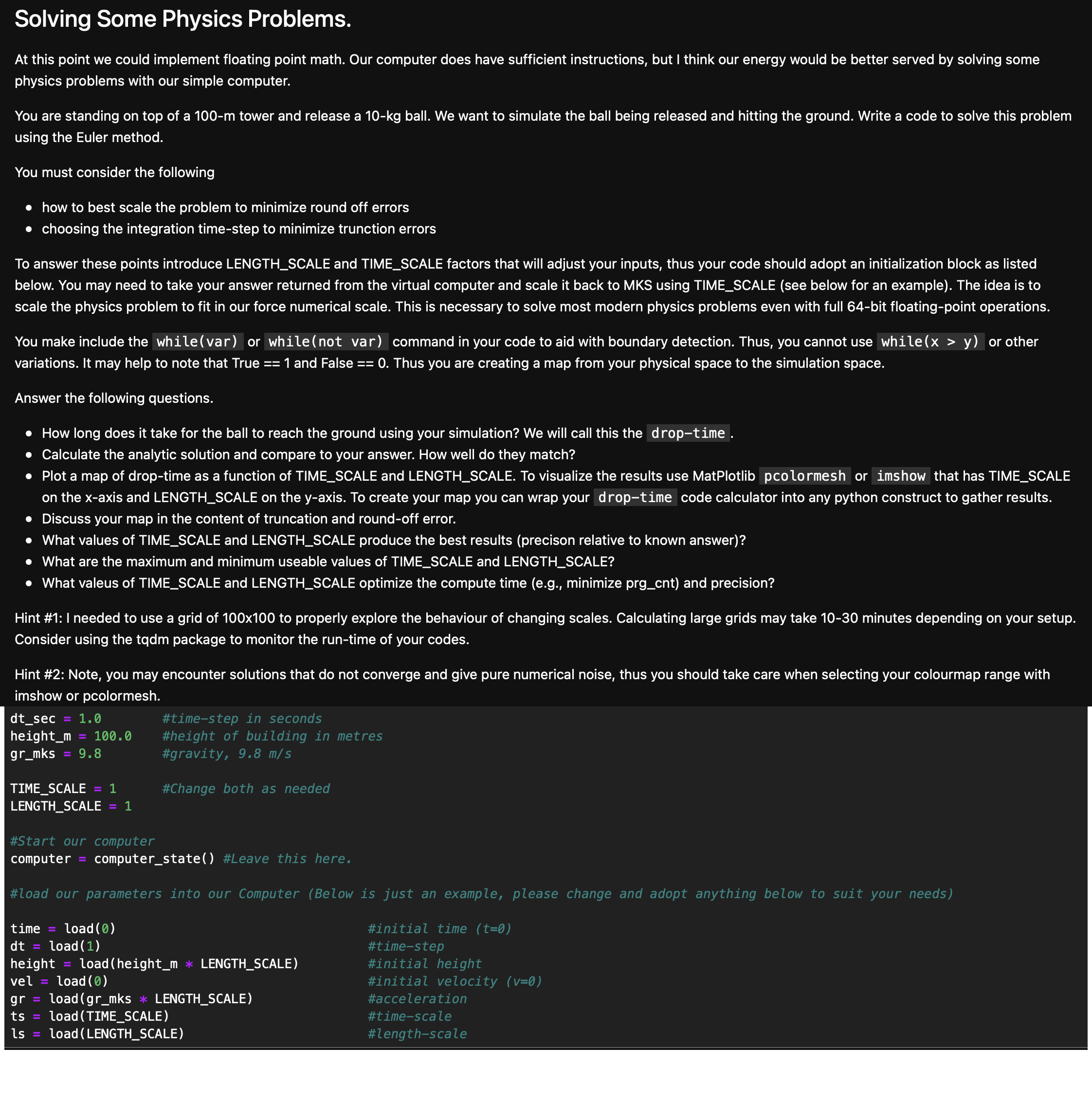
dt$\_$sec $=1\mathrm{.}0,$ #time$-$step in seconds

height$\_$m $=100\mathrm{.}0,$ #height of building in metres

gr$\_$mks $=9\mathrm{.}8,$ #gravity, $9\mathrm{.}8\frac{m}{s}$

TIME$\_$SCALE $=1,$ #Change both as needed

LENGTH$\_$SCALE $=1$

#Start our computer

computer $=$ computer$\_$state$()$ #Leave this here.

#load our parameters into our Computer $($Below is just an example, please change and adopt anything below to suit your needs$)$

time $=$load$(0)$

$dt=$load$(1)$

height $=$ load$($height$\_m**$ LENGTH$\_$SCALE$)$

vel $=$load$(0)$

gr $=$ load $($gr$\_$mks $**$ LENGTH$\_$SCALE$)$

ts $=$ load$($TIME$\_$SCALE$)$

#initial time $(t=0)$

#time$-$step

#initial height

#initial velocity $(v=0)$

#acceleration

ls $=$ load$($LENGTH$\_$SCALE$)$

#time$-$scale

#length$-$scale