some code to that I have but lost

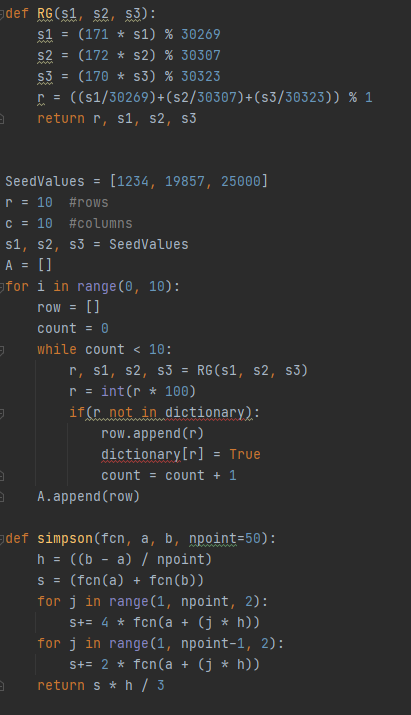
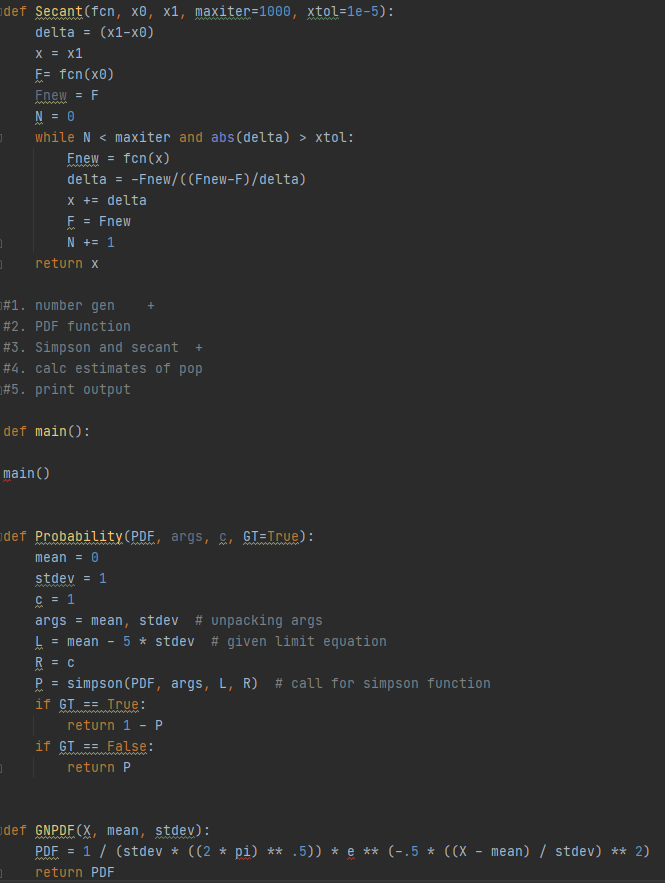
Please Help me with this because I am lost right now!

I just realized that the def probability is not needed in this so please look past that

Use your pseudorandom number generator from question 4 to generate a list of 1000 random floating point numbers between 0 and 1 (duplicates are okay). Consider these values to represent probability levels that can be found by integrating the Gaussian probability density function (PDF) between x=u-5.0 to x=x; such that pi=P(x xtol: Fnew = fon(x) delta = -Fnew/((Fnew-F)/delta) X += delta F = Fnew N += 1 return x #1. number gen #2. PDF function #3. Simpson and secant #4. calc estimates of pop #5. print output + def main(): main() def Probability. (PDF, args, C GT=True): mean = 0 stdev = 1 = 1 args = mean, stdev # unpacking args = mean - 5 * stdev # given limit equation R = C P = simpson (PDF, args, L, R) # call for simpson function if GT == True: return 1 - P if GT == False: return P def GNPDFCX, mean, stdev): PDF 1 / (stdev * ((2 * pi) ** .5)) * e ** (-.5 * ((X - mean) / stdev) ** 2) return PDF Use your pseudorandom number generator from question 4 to generate a list of 1000 random floating point numbers between 0 and 1 (duplicates are okay). Consider these values to represent probability levels that can be found by integrating the Gaussian probability density function (PDF) between x=u-5.0 to x=x; such that pi=P(x xtol: Fnew = fon(x) delta = -Fnew/((Fnew-F)/delta) X += delta F = Fnew N += 1 return x #1. number gen #2. PDF function #3. Simpson and secant #4. calc estimates of pop #5. print output + def main(): main() def Probability. (PDF, args, C GT=True): mean = 0 stdev = 1 = 1 args = mean, stdev # unpacking args = mean - 5 * stdev # given limit equation R = C P = simpson (PDF, args, L, R) # call for simpson function if GT == True: return 1 - P if GT == False: return P def GNPDFCX, mean, stdev): PDF 1 / (stdev * ((2 * pi) ** .5)) * e ** (-.5 * ((X - mean) / stdev) ** 2) return PDF