Square Roots Via Iteration

You are to write a program which will compute square roots to a desired degree of accuracy. Begin the program by prompting the user for two numbers: (1) the value for which to determine the square root and (2) the number of decimal places of accuracy desired in the result. For example, find the square root of 7 to four decimal places; the actual value is 2.6458.

The first computational step is to use event-controlled loops to find the next smaller and next larger square roots as discussed in this week's in-lab exercises. The average of these two values is then used as the first approximation of the desired square root. Continuing the example, the next smaller and next larger square roots are 2 and 3, respectively, as their squares, 4 and 9, bracket 7; consequently, the first approximation is 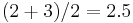, not far from the actual value in this case.

A count-controlled loop should then be constructed; it will execute once for each of the desired decimal positions; in the example, this loop will execute four times (once each for the tenths, hundredths, thousandths, and ten-thousandths decimal positions). Use a counter such as decimalPosition to keep track of which pass the loop is on.

During a single pass of this count-controlled loop, the approximation will be either incremented or decremented by 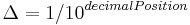until the actual value is passed. On the first pass of the loop, will be 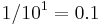; on the second pass, will be 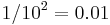, and so on.

If the approximation is too small, as in the example, an event-controlled loop inside the count-controlled loop will increment the approximation until it becomes too big; in the example, during the first pass of the count-controlled loop, 2.5 is incremented to 2.6 and then to 2.7, at which point it can be determined that 2.7 is too large. Making this decision is done by simply squaring the approximation and comparing to the original value. In the example, 2.5*2.5 = 6.25, which is less than 7; 2.6*2.6 = 6.76, which is also too small; finally, 2.7*2.7 = 7.29, which is too large. It is now clear that the square root for 7 must lie between 2.6 and 2.7.

In the example, the second pass of the count-controlled loop will start with an approximation of 2.7, which has already been seen to be too large. The count-controlled loop's is now 0.01; a second event-controlled loop is now needed to decrement the approximation until it becomes too small. In the example, the approximation 2.7 is decremented to 2.69, then 2.68, and so on down to 2.63 at which point it has become too small again.

The third pass of the count-controlled loop, with = 0.001, will refine the third decimal position using the first of the two event-controlled loops above. Each successive pass of the count-controlled loop refines one more decimal position.

The accuracy of the C++ type double is limited to approximately fifteen digits in the current implementation; note that these include digits to both sides of the decimal position. Warn the user of the program about this limitation in the prompt for the desired accuracy at the beginning of the program.

On each pass of the inner event-controlled loops, display the current value of , the current approximation to the square root, and the error associated with the approximation. The error is the difference between the number for which the square root is being approximated and the square of the approximation. Sample results for the square root of 7 to four decimal places follow.

Example of expected output.

Find the square root of 7 to 4 decimal places. approx delta sq root error ----- ------- ----- 2.5000 0.1000 2.6000 0.2400 0.1000 2.7000 -0.2900 0.0100 2.6900 -0.2361 0.0100 2.6800 -0.1824 0.0100 2.6700 -0.1289 0.0100 2.6600 -0.0756 0.0100 2.6500 -0.0225 0.0100 2.6400 0.0304 0.0010 2.6410 0.0251 0.0010 2.6420 0.0198 0.0010 2.6430 0.0146 0.0010 2.6440 0.0093 0.0010 2.6450 0.0040 0.0010 2.6460 -0.0013 0.0001 2.6459 -0.0008 0.0001 2.6458 -0.0003 0.0001 2.6457 0.0003 The square root of 7 to 4 decimal places is 2.6457. The approximation 2.6457 squared is 6.9997. The actual square root of 7 to 5 decimal places is 2.64575. 

Recall that the iomanip library contains manipulators to format output. At some point prior to the count-controlled loop, use fixed and setprecision(p) to indicate that floating point results should be displayed in a fixed number format, (nn.nnn and not n.nnE+nn), and that p decimal positions should be shown, even if all are trailing zeroes. This need only be done once as fixed and setprecision will remain in effect until reset.

Use setw(w) to display a value in a total of w columns; this must be done for each individual value.

Please give answer in C++ language.

(2 +3)/2 2.5