Standard normal table:

Only parts d and e need an answer. 710.16 is an incorrect answer for part d.

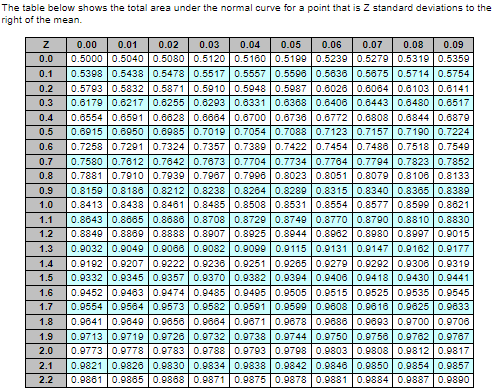
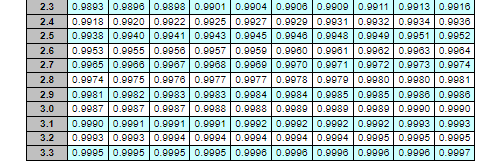
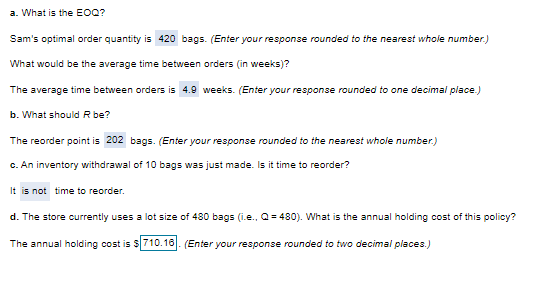
Sam's Cat Hotel operates 52 weeks per year, 7 days per week, and uses a continuous review inventory system. It purchases kitty litter for $11.25 per bag. The following information is available about these bags. Refer to the standard normal table for z-values. > Demand = 85 bags/week > Order cost = $56/order > Annual holding cost = 25 percent of cost > Desired cycle-service level = 92 percent > Lead time = 2 week(s) (14 working days) > Standard deviation of weekly demand = 16 bags > Current on-hand inventory is 350 bags, with no open orders or backorders The table below shows the total area under the normal curve for a point that is Z standard deviations to the right of the mean. 0.04 Z 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 0.00 0.01 0.02 0.03 0.05 0.06 0.07 0.08 0.09 0.5000 0.5040 0.5080 0.5120 0.51600.5199 0.5239 0.52790.5319 0.5359 0.5398 0.5438 0.5478 0.5517 0.5557 0.5598 0.5836 0.5875 0.5714 0.5754 0.5793 0.58320.58710.5910 0.5948 0.5987 0.6026 0.8064 0.8103 0.6141 0.61790.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.65540.6591 0.6628 0.68640.6700 0.6736 0.6772 0.6808 0.68440.6879 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 0.7258 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.75180.7549 0.7580 0.7612 0.76420.7673 0.7704 0.77340.7764 0.77940.7823 0.7852 0.7881 0.79100.7939 0.7967 0.7996 0.8023 0.8051 0.8079 0.8106 0.8133 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.8389 0.8413 0.8438 0.8481 0.8485 0.8508 0.8531 0.85540.85770.8599 0.8621 0.86430.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.89620.89800.8997 0.9015 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 0.91920.9207 0.9222 0.9238 0.9251 0.9205 0.9279 0.9292 0.9306 0.9319 0.9332 0.9345 0.9357 0.9370 0.93820.9394 0.9406 0.9418 0.9430 0.9441 0.94520.9463 0.9474 0.9485 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 0.9554 0.9584 0.9573 0.9582 0.9591 0.9599 0.9808 0.9816 0.9625 0.9833 0.9641 0.9649 0.9656 0.9864 0.9671 0.9678 0.9686 0.9893 0.9700 0.9706 0.97130.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.97560.9762 0.9767 0.97730.9778 0.9783 0.9788 0.9793 0.9798 0.98030.9808 0.98120.9817 0.9821 0.9826 0.9830 0.98340.98380.98420.9846 0.9850 0.9854 0.9857 0.9881 0.98650.9868 0.98710.98750.9878 0.9881 0.9884 0.9887 0.9890 ITT 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 0.9893 0.9896 0.9898 0.9901 0.99040.9906 0.9909 0.99110.99130.9916 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.99320.99340.9936 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 0.9953 0.9955 0.9956 0.9957 0.99590.9960 0.9981 0.99620.9963 0.9984 0.9965 0.9986 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974 0.99740.9975 0.9978 0.9977 0.99770.9978 0.9979 0.99800.99800.9981 0.9981 0.99820.9983 0.9983 0.99840.99840.9985 0.9985 0.9986 0.9986 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.99920.9993 0.9993 0.9993 0.9993 0.9994 0.9994 0.9994 0.99940.99940.9995 0.9995 0.9995 0.9995 0.9995 0.9995 0.9995 0.9998 0.9997 0.9996 0.9996 0.9996 0.9997 3.3 a. What is the EOQ? Sam's optimal order quantity is 420 bags. (Enter your response rounded to the nearest whole number.) What would be the average time between orders (in weeks)? The average time between orders is 4.9 weeks. (Enter your response rounded to one decimal place.) b. What should be? The reorder point is 202 bags. (Enter your response rounded to the nearest whole number.) c. An inventory withdrawal of 10 bags was just made. Is it time to reorder? It is not time to reorder. d. The store currently uses a lot size of 480 bags (i.e., Q = 480). What is the annual holding cost of this policy? The annual holding cost is $710.16. (Enter your response rounded to two decimal places.) e. What would be the annual cost saved by shifting from the 480-bag lot size to the EOQ? The annual holding cost is