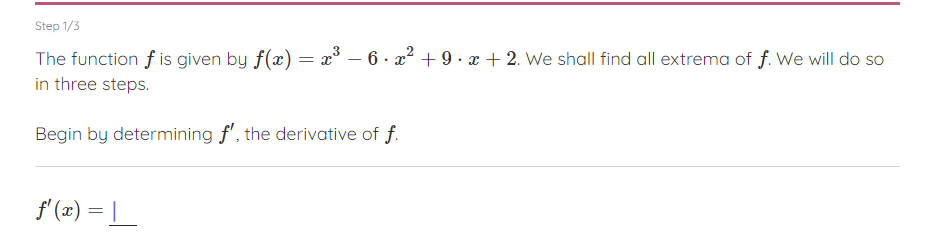
Step 1,15 The function f is given lag x) 2 2:3 6 - m2 l 9 ' :1: + 2. We shall find all extrema at I. We will do so in three steps. Begin by determining f', the derivative at I. Has} = |_ Step 2/3 In the previous step, we saw that the function f(a) = a - 6 . x + 9 . a + 2 has derivative f'(a) = 3x2 - 12x + 9. We want to find all extrema of f. By the theory, these will be zeros of f. Find the two zeros of f. Name the smallest value x_ and the biggest value :4.Step 3/3 In the previous step we saw that the zeros of the derivative f of the function f(x) = -6 . x +9 .x+2arex_=1andx = 3. Which of the following statements regarding the function f are true? At 1 the function f has a local minimum At 3 the function f has a local maximum