Question: Step 7: We will make one more function, 'r(n) that will approximate the area for any given number of rectangles. r[n_]:=NSum[f[x[i,0,3,n]]*delta[0,3,n], {i,1,n}] Then press ?
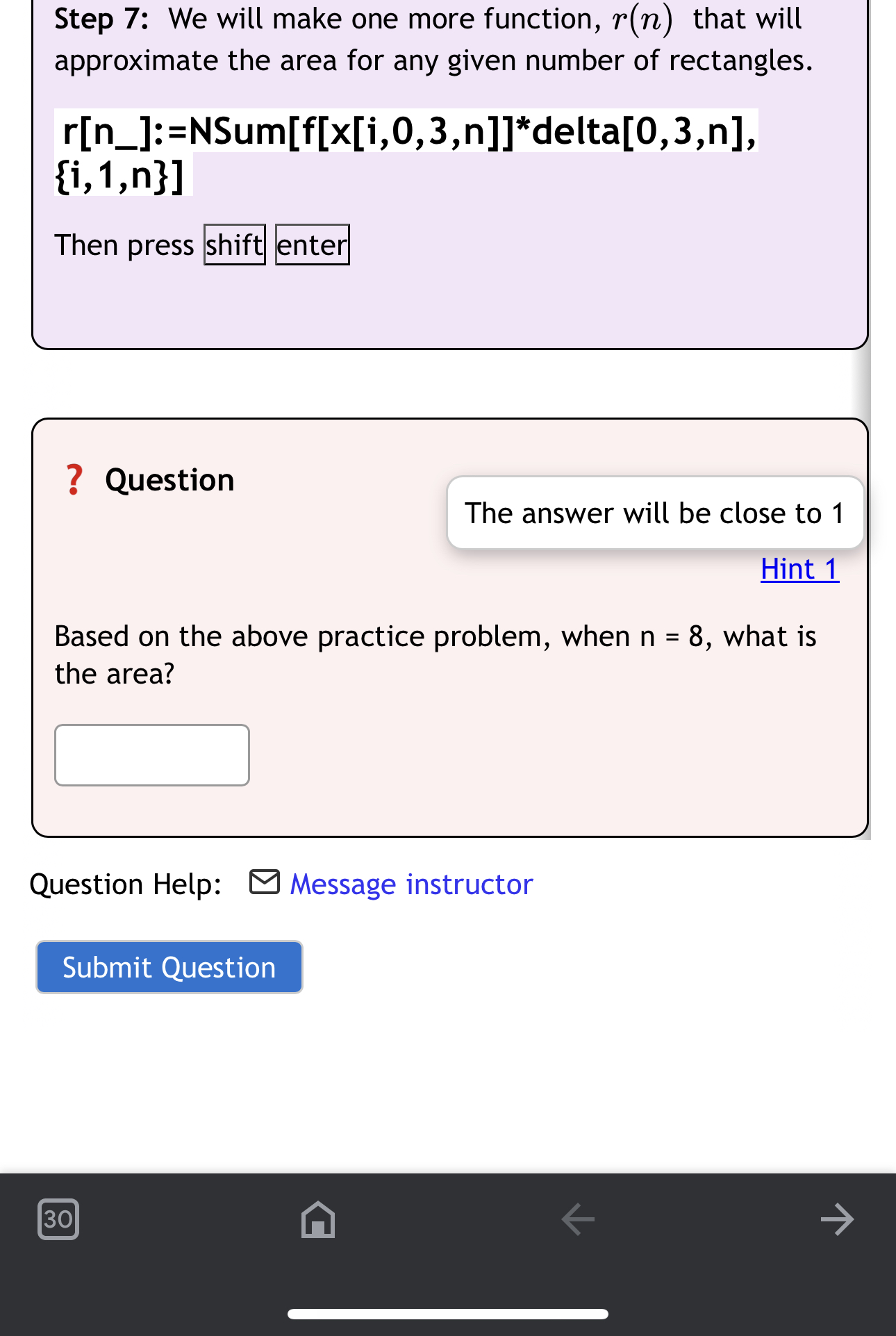
![approximate the area for any given number of rectangles. r[n_]:=NSum[f[x[i,0,3,n]]*delta[0,3,n], {i,1,n}] Then](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66670ae251233_02666670ae21e2a5.jpg)
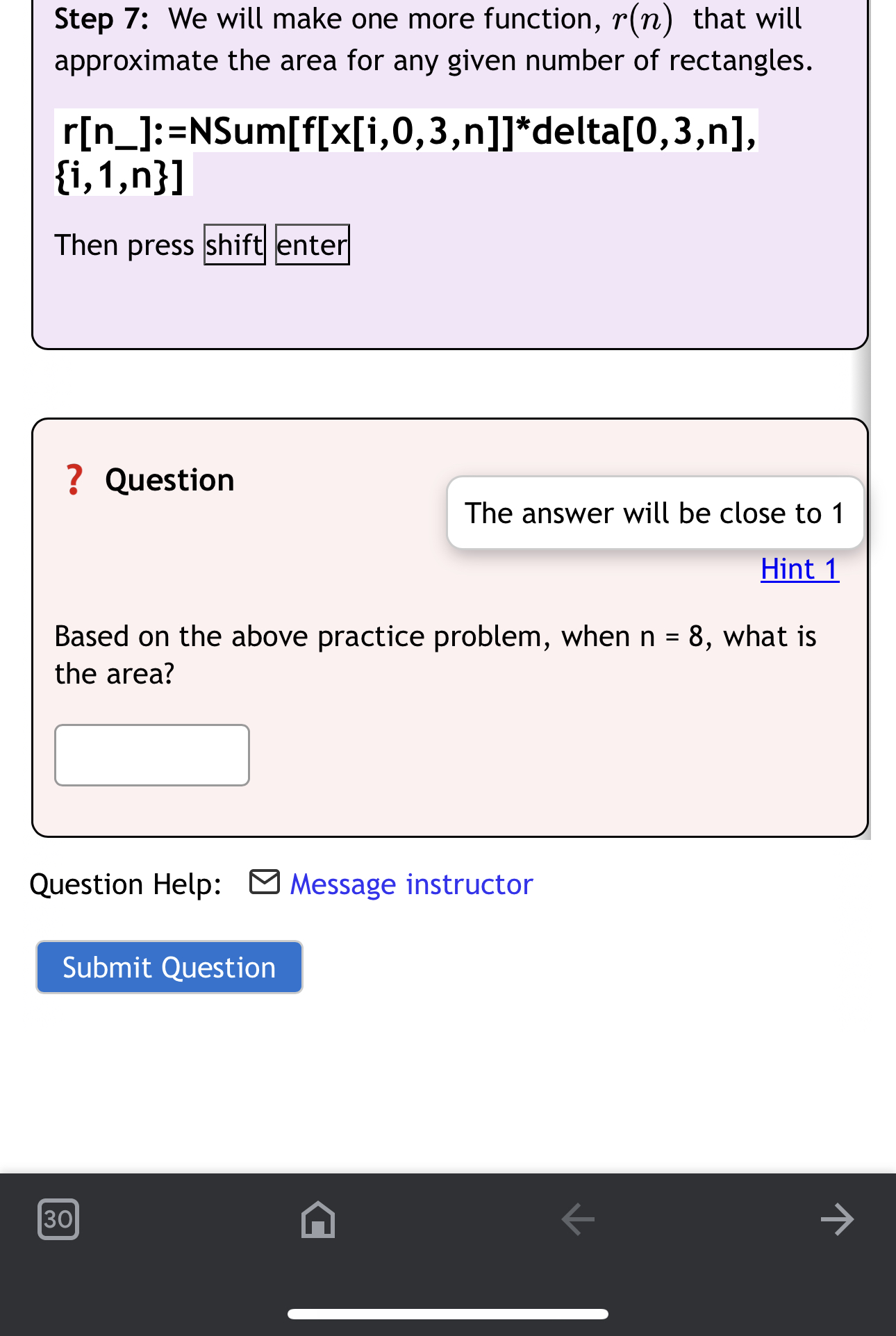
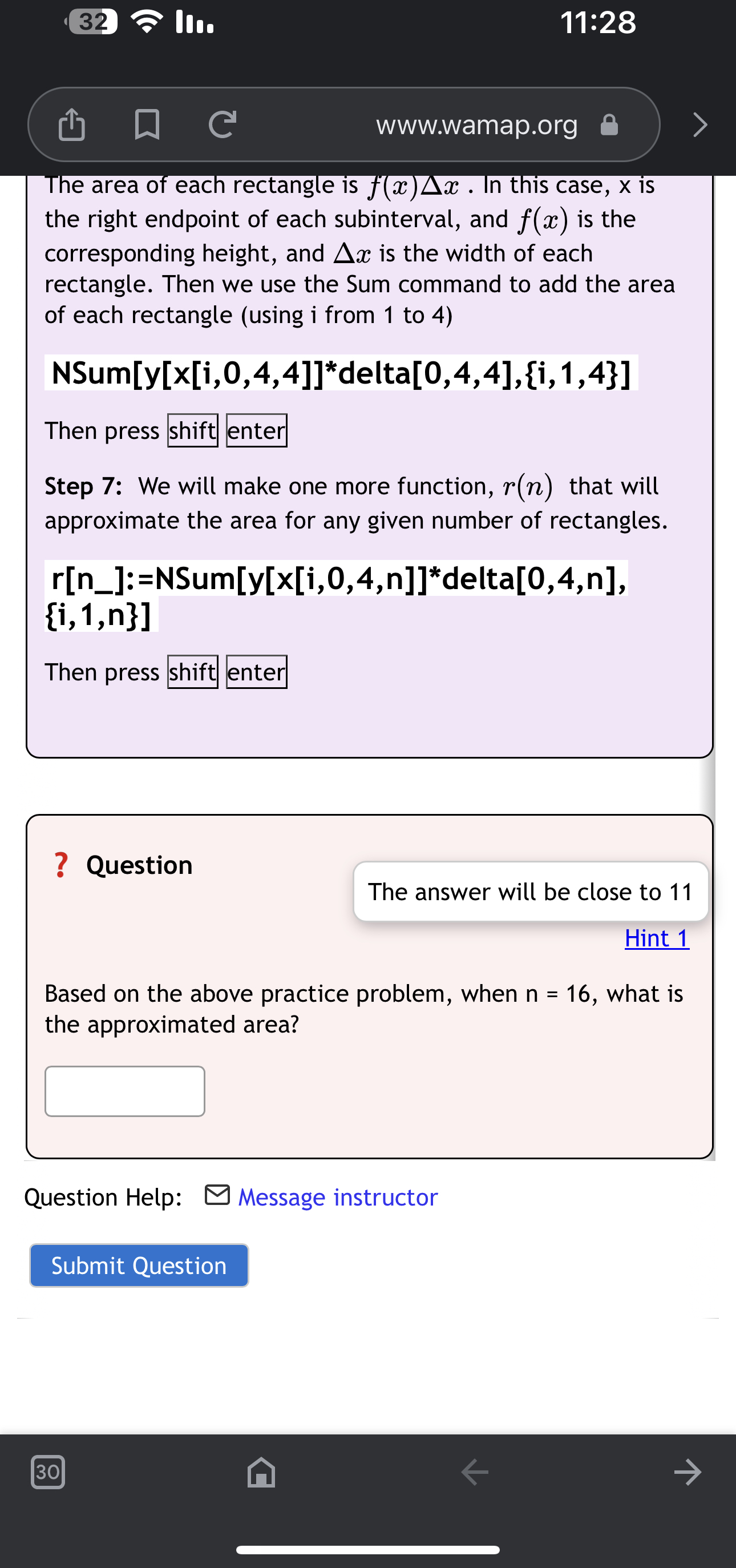
Step 7: We will make one more function, 'r(n) that will approximate the area for any given number of rectangles. r[n_]:=NSum[f[x[i,0,3,n]]*delta[0,3,n], {i,1,n}] Then press ? Question The answer will be close to 1 Hint 1 Based on the above practice problem, when n = 8, what is the area? Question Help: 8 Message instructor Submit Question 11:28 www.wamap.org B e area 0 eac rectang e IS . n t is case, x is the right endpoint of each subinterval, and f(33) is the corresponding height, and A13 is the width of each rectangle. Then we use the Sum command to add the area of each rectangle (using i from 1 to 4) NSum[y[x[i,O,4,4]]*delta[0,4,4],{i,1,4}] Then press Step 7: We will make one more function, r(n) that will approximate the area for any given number of rectangles. r[n_]:=NSum[y[x[i,0,4,n]]*delta[0,4,n], {i,1,n}] Then press ? Question The answer will be close to 11 Hint 1 Based on the above practice problem, when n = 16, what is the approximated area? Question Help: 8 Message instructor Submit
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


