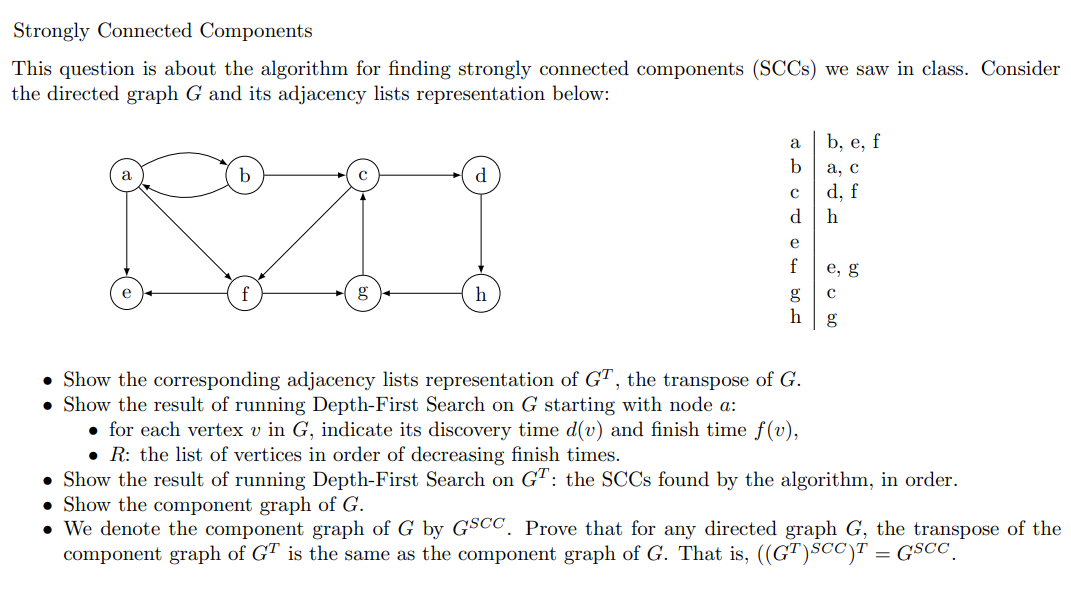
Strongly Connected Components This question is about the algorithm for finding strongly connected components (SCCs) we saw in class. Consider the directed graph G and its adjacency lists representation below: \begin{tabular}{l|l} a & b,e,f \\ b & a,c \\ c & d,f \\ d & h \\ e & \\ f & e,g \\ g & c \\ h & g \end{tabular} - Show the corresponding adjacency lists representation of GT, the transpose of G. - Show the result of running Depth-First Search on G starting with node a : - for each vertex v in G, indicate its discovery time d(v) and finish time f(v), - R : the list of vertices in order of decreasing finish times. - Show the result of running Depth-First Search on GT : the SCCs found by the algorithm, in order. - Show the component graph of G. - We denote the component graph of G by GSCC. Prove that for any directed graph G, the transpose of the component graph of GT is the same as the component graph of G. That is, ((GT)SCC)T=GSCC