Subject is : numrical analysis ..

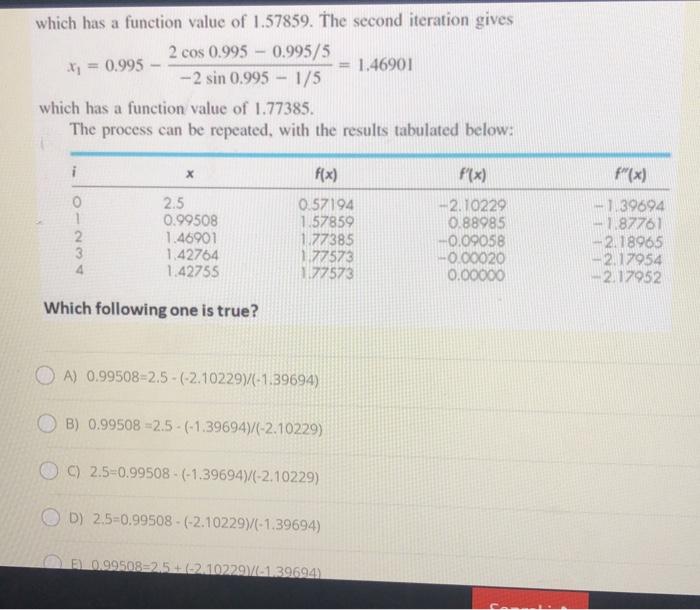
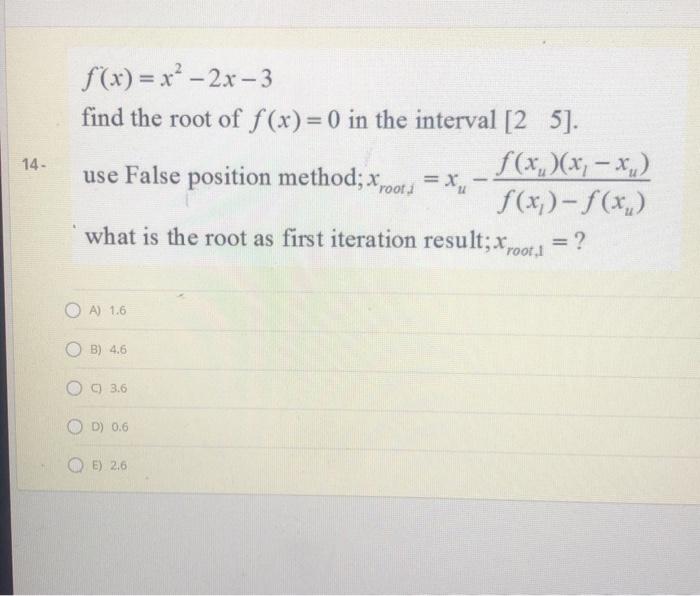
39- dy = f(x, y) = x + y2, y(1) = 5 dx find y(3) value by euler method, take step size; h=1. A) 200 B) 20200 1000 D) 500 E) 100 which has a function value of 1.57859. The second iteration gives 2 cos 0.995 - 0.995/5 1.46901 - 2 sin 0.995 - 1/5 which has a function value of 1.77385. The process can be repeated, with the results tabulated below: Xy = 0.995 - i X f(x) "(x) o 1 2 3 2.5 0.99508 1.46901 1.42764 1.42755 f(x) 0.57194 1.57859 1.77385 177573 177573 -2.10229 0.88985 -0.09058 -0.00020 0.00000 -139694 -1.87761 -2.18965 -2.17954 -2.17952 Which following one is true? A) 0.99508=2.5 - (-2.10229)/(-1.39694) B) 0.99508 -2.5-(-1.39694)/(-2.10229) OC) 2.5=0.99508- (-1.39694)/(-2.10229) OD) 2.5=0.99508 - (-2.10229)/(-1.39694) 0.99508325+ 22.10229-139694) 14- f(x) = x2 - 2x - 3 find the root of f(x) = 0) in the interval [25]. use False position method; xroot a = x, f(x)(x, x,) f(x)-f(x,) what is the root as first iteration result; xroot4 = ? A) 1.6 B) 4.6 C) 3.6 D) 0.6 E) 2.6