Question: Subject: Numerical Methods Topic: System of Linear Equations - Direct Methods Please refer to the guides. Also kindly provide a complete solution. Thank you Each
Subject: Numerical Methods
Topic: System of Linear Equations - Direct Methods
Please refer to the guides. Also kindly provide a complete solution. Thank you
Each Part has their own name and number.
-Worksheet 5
-Brain Exercises 1,4,6,8,10
-Brain Provokers 1,2,3
-Mind Strainers 1,3,5,7,9

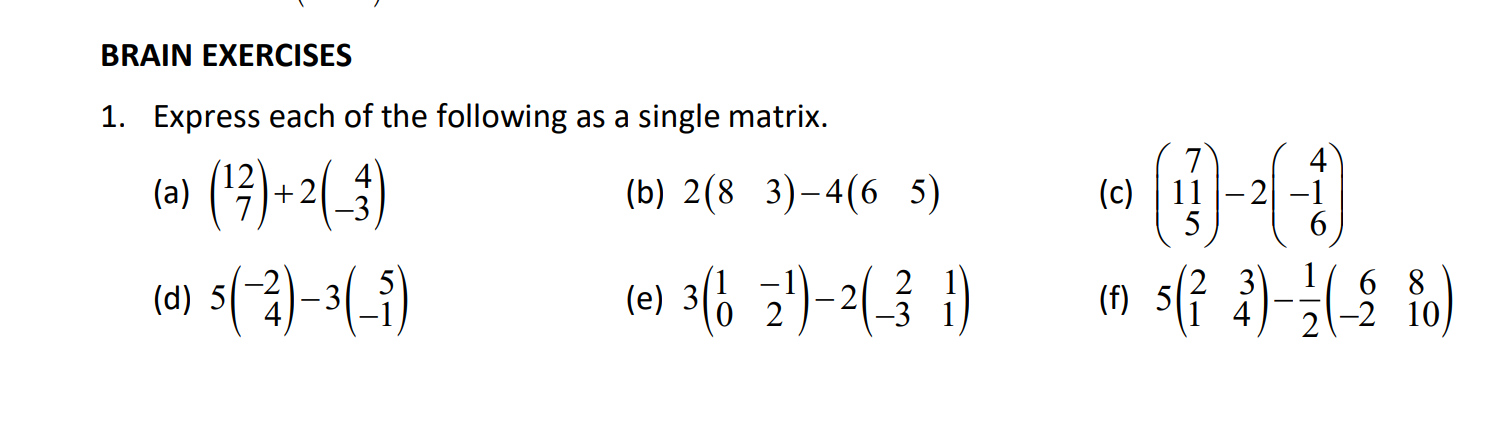
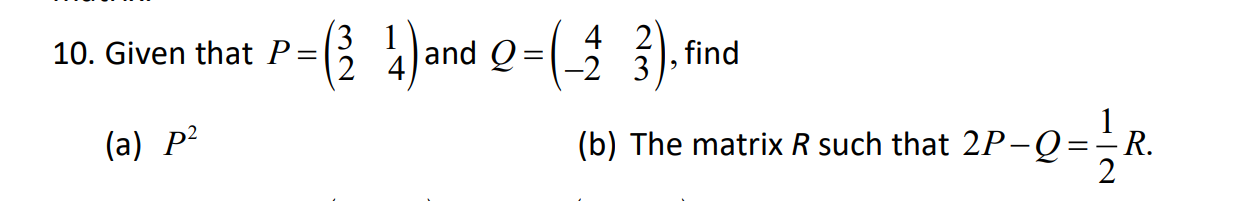
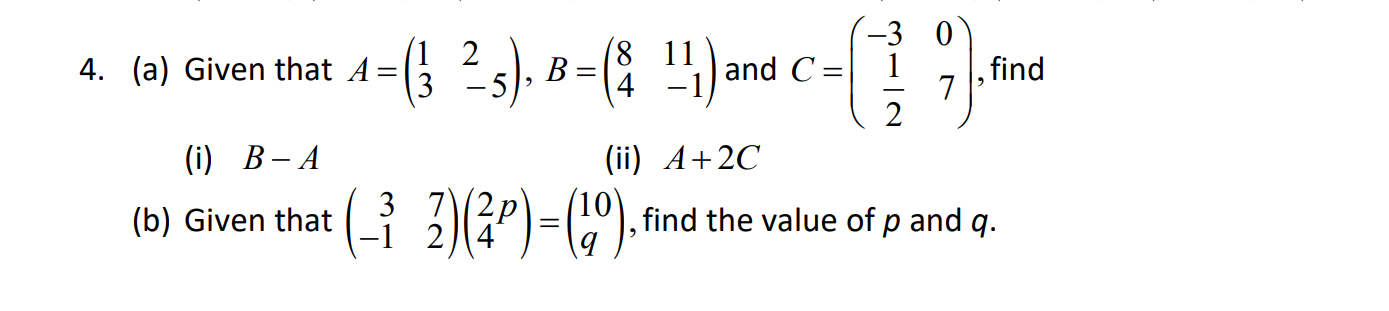
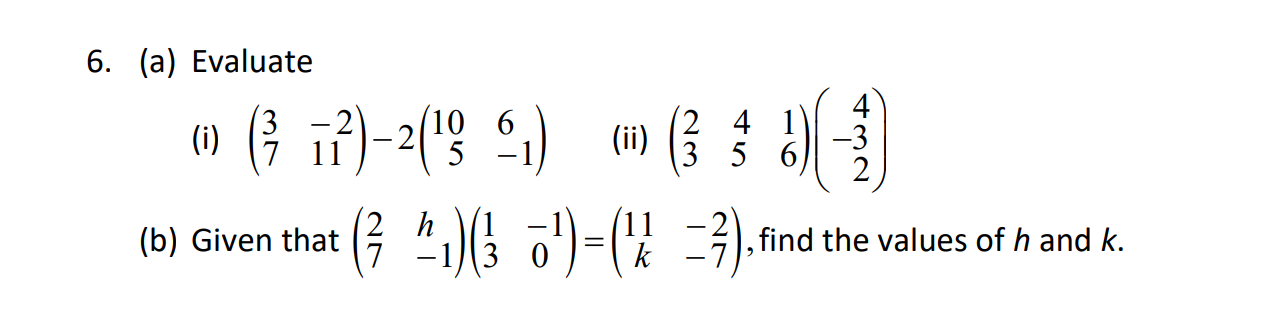
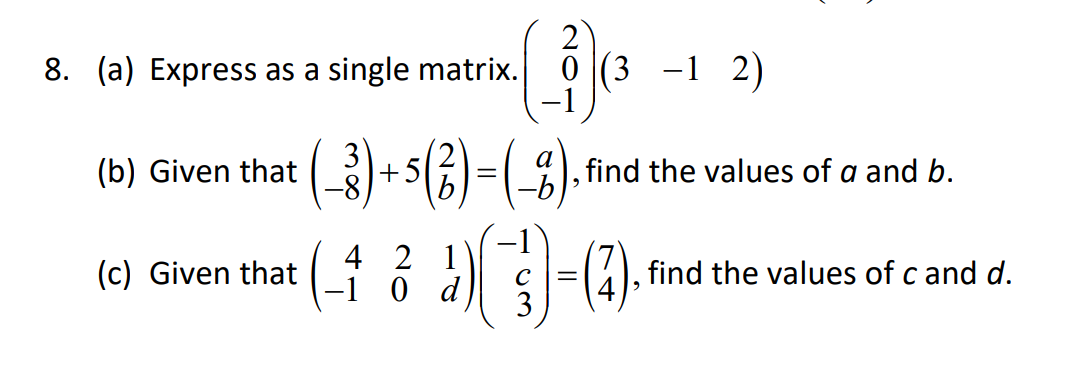
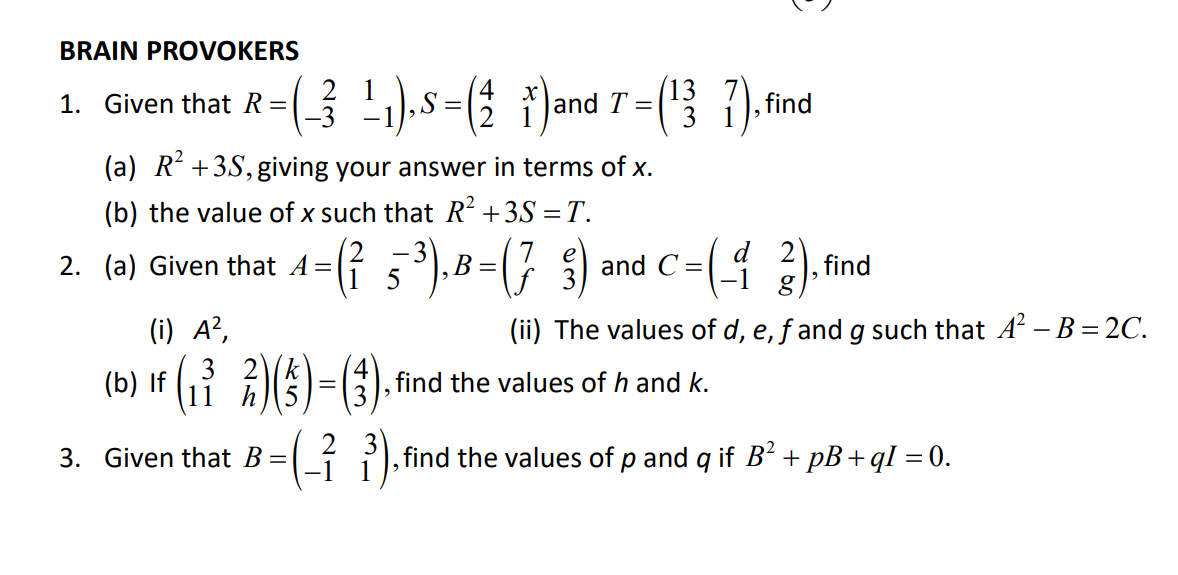

 (b) Given that ( 3)+2(5b)_ (),f ind the](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6703ef373de57_0956703ef3722d5e.jpg)

![]=(4) )find the values of c and d. mallI BRAIN PROVOKERS 1.](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6703ef382bd3b_0956703ef3801066.jpg)

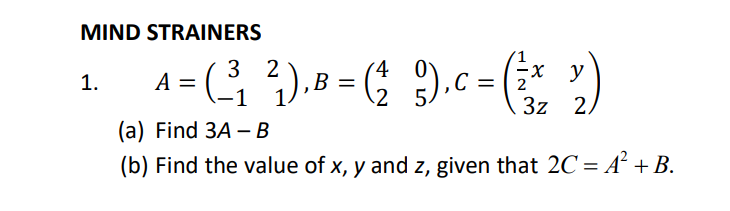
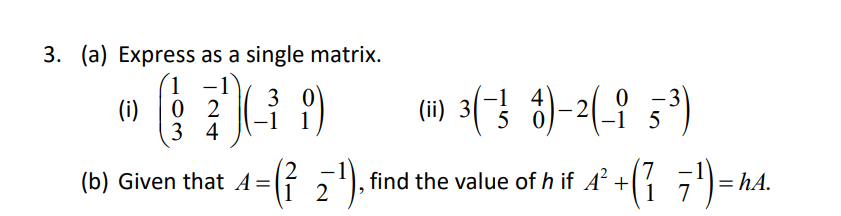
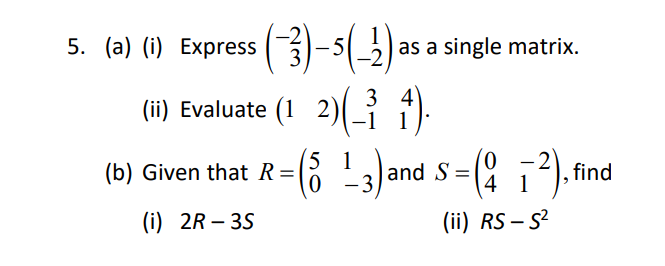
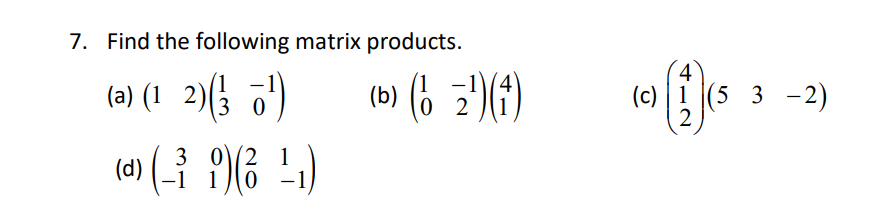
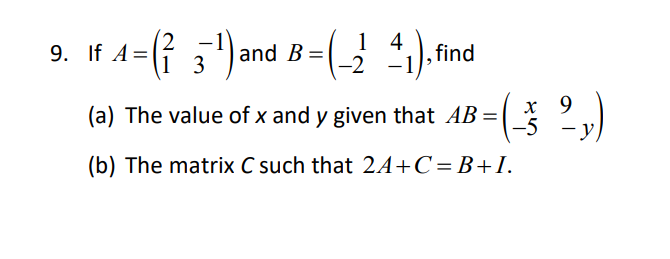
Provide a detail solution per each number. [a - 2013 a a + 2013 1. Show that b b + 2013 b + 4026 =0. c + 2013 c + 4026 c + 6039 a b+c a+ bl 2. Prove that the determinant of cta b+c = a3+b3+ c3 - 3abc. C atb ctal\f\f\f\f2 8. (a) Express as a single matrix.[ (1)](3 1 2) (b) Given that ( 3)+2(5b)_ (),f ind the values of a and b. a (b (c) Given that( _1 M[ ]=(4) )find the values of c and d. mallI BRAIN PROVOKERS 1. Given that R = 3 1 1),S=(2 { )and T = (13 7), find (a) R' + 3S, giving your answer in terms of x. (b) the value of x such that R2 + 3S = T. 2. (a) Given that A = 7 53 ) , B= ( 7 3) and C =( 9 ), find (i) A2, (ii) The values of d, e, f and g such that A - B = 2C. (b) If i h)( 5 ) = WA find the values of h and k. 3. Given that B = 2 -1 1 , find the values of p and q if B2 + pB + ql = 0.MATRICES A matrix (plural matrices) is a set of numbers, called elements arranged in a rectangular array. 1 Example G '24){9 Jand [% 0.1 20] are matrices. The order of a matrix describes the number of rows and the number of columns if contains. A m x 11 matrix has m rows and n columns. Example (g) is a 2 X 1 matrix. ( The order ofthe matrix is 2 by 1, that is it has 2 rows and 1 column. (g 3) is a 2x2matrix. (1 4 7) is a 1 x 3 matrix. A row matrix has exactly one row. Its order is 1 x n, where n is the number of columns. Example (1 2) is a 1 x 2 matrix. (3 9 7) is a 1 x 3 matrix. A column matrix has exactly one column. Its order is m x 1, where m is the number of rows. Example (15)\"; a 2 x 1 matrix. 8 [I] is a 3 x 1 matrix. 3 A square matrix has the same number of rows and columns. Example (6) is a 1 x 1matrix. AN is a 2 x 2 matrix. 0 2 is a 3 x 3 matrix. 4 A zero matrix or a null matrix has all its elements equal to zero. It is denoted by 0. A zero matrix can be of any order. Example (0), (8 9) and (0 0 0) are identify matrices. An identify matrix is a square matrix in which all the elements in the leading diagonal are equal to 1 and the rest of the elements are equal to zero. It is denoted by I. 0 O Example (6 9) and O are identify matrices. 0 If A and B are two matrices of the same order and their corresponding elements are equal. Example (2 6) -(2 61) while (1 8) #ADDITION AND SUBTRACTION OF MATRICES 1. We can add or subtract two matrices if both are the same order. 2. To add or subtract matrices, add or subtract the corresponding elements. Example 1 (1 3) + (5 -1) = (6 2) Example 2 (71 8)-(31 7) -(12 6) In general, if A = (a b) and B = (9 ,), then ( ate b+f) A+B=( a) +(8 h)=(c+g dth 4-B= (a b ) - (8 4) = ( 9-8 6 4 ) 3. Matrix addition is commutative. A+ B = B+ A Example (2 ) + (3) =(8) )+ (2 ) =1 4. Matrix addition is associative. ( A+ B) + C= A+(B+C)= A+B+C Example (2) (8) =1PRODUCT 0F SCALAR QUANTITY AND A MATRIX To multiply a matrix by a real number, k, multiply ever element in the matrix by k. Example A:(_% g] 214:2(_11 3) 3mm 3H? 2) gen 3)= r In general, if A = (g 3)and k is any real number, then _ a b _ ka kb "Ak(c d)_(kc kd) MULTIPLICATION OF MATRICES 1- We can multiply two matrices together if the number of columns in the first matrix is equal to the number of rows in the second matrix. In general, two matrices A (order m x n) and B (order p x q) can be multiplied together only if n = p. The result will be a matrix of order m x q. Emmi %)(12)=[i::3:ii:3)=(a:)=(a) Order:2xx1 2x1 2 4 1 3 _ 2x1+ 4x2) (2x3)+(4x0) _ 10 6 Exam"? 2 [0 1N2 0)_[0x1;+flx2) (0x3)+{1x0) 2 0 a If A is a square matrix of order n x n and | is the identify matrix of the same order, then AI=I =A ha. MIND STRAINERS 1. A 3 2 2 1 1) . B = (2 3 ).C= 3z 2 (a) Find 3A - B (b) Find the value of x, y and z, given that 2C = A + B.3. (a) Express as a single matrix. (i) (11 ) 3 ( - 3 4 ) -21 9 5 (b) Given that A = 2 -1 1 2 , find the value of h if A + 7 - = hA.5. (a) (i) Express WN -5 as a single matrix. (ii) Evaluate (1 2) (_ f) (b) Given that R = ( 3) and S = (9 2), find (i) 2R - 35 (ii) RS - S27. Find the following matrix products. (a) (1 2) 3 (b) ( 6 2!) (4 ) (c) | 1 NED (5 3 - 2 )9. If A= (7 3 ) and B=(_2 -1), find X 9 (a) The value of x and y given that AB = -5 - V (b) The matrix C such that 2A+ C = B+I
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


