Suppose a certain state function S has the following differential form. ds=(Cv/T)dT-(B/k)dv Where B is the coefficient of thermal expansion, B=(1/v)(V...(see picture) k is the coefficient of isothermal compressibility (k=... see picture) and Cv is the heat capacity at constant volume . Using the properties of exact differentials, we can obtain the following relations from this differential form.

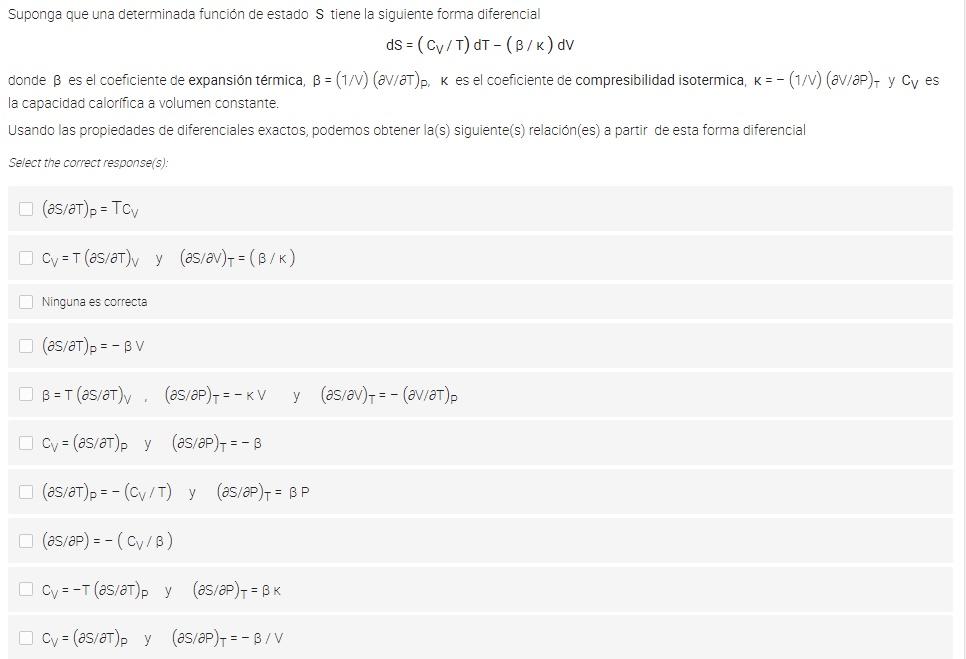
Suponga que una determinada funcin de estado S tiene la siguiente forma diferencial ds = (CV/T) dT - (B/K) av donde B es el coeficiente de expansin trmica, B = (1/0) (av/at)p, K es el coeficiente de compresibilidad isotermica, k=-(1/0) (av/aP), y Cy es la capacidad calorifica a volumen constante. Usando las propiedades de diferenciales exactos, podemos obtener la(s) siguiente(s) relacin(es) a partir de esta forma diferencial Select the correct response(s): (as/at), = Toy Cv = T (as/at)y y (as/av) = (B/K) Ninguna es correcta (as/at) = - BV B = T (as/aT). (as/P)-=-KV y (as/av), = -(aviat). Cv = (as/at) py (as/aP) = - B (as/at)p=-(C/T) y (as/aP)1 = BP (as/aP) =-(C/B) Ov=-T (as/at)py (as/aP)1 = BK cv = (as/at). y (as/aP)-=-B/V