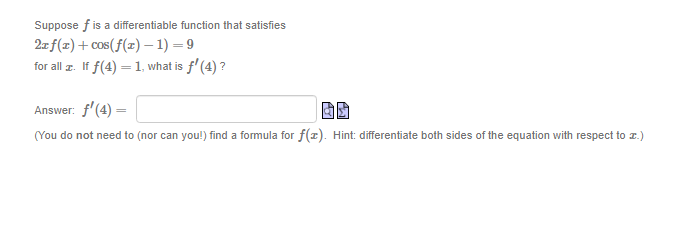
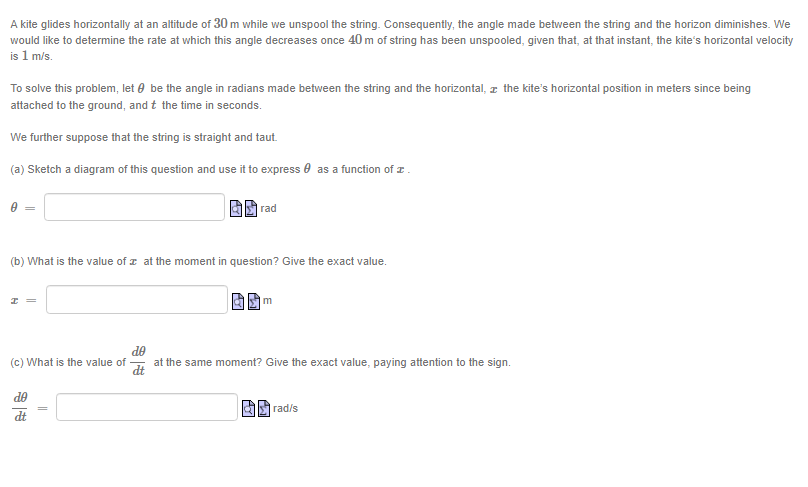
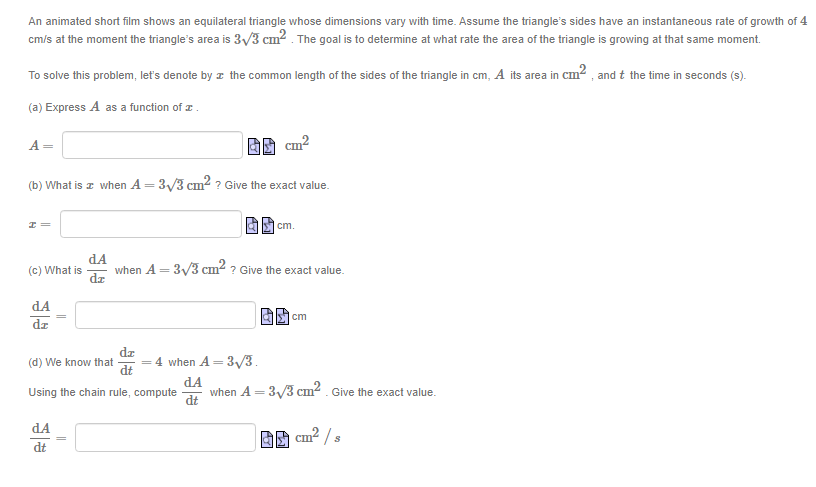
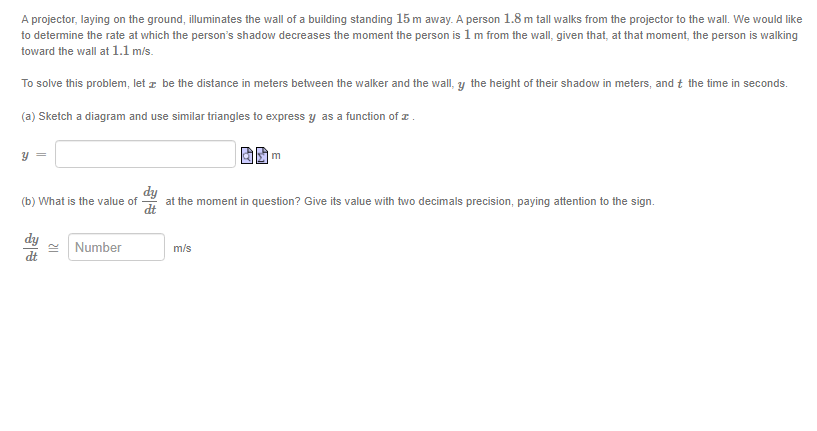
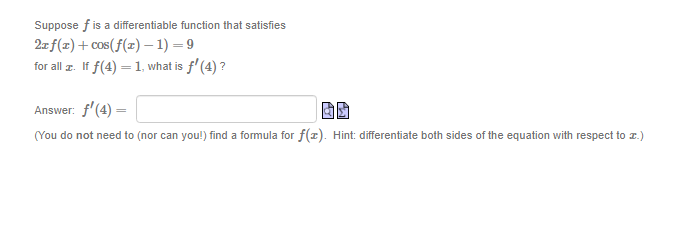
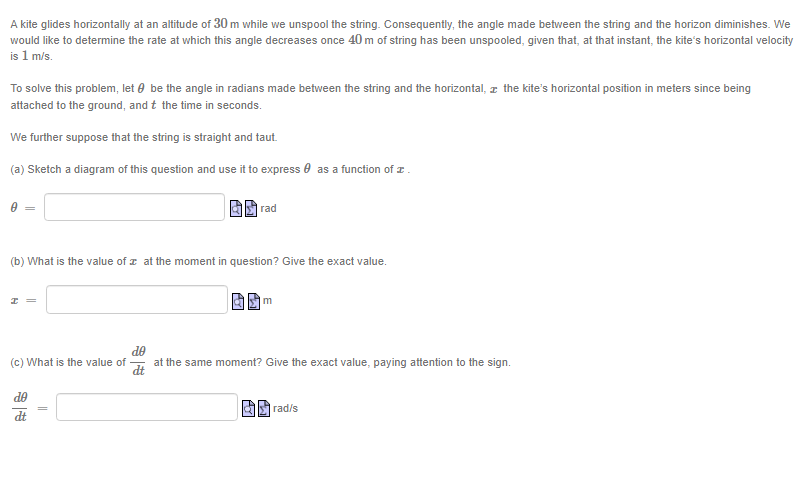
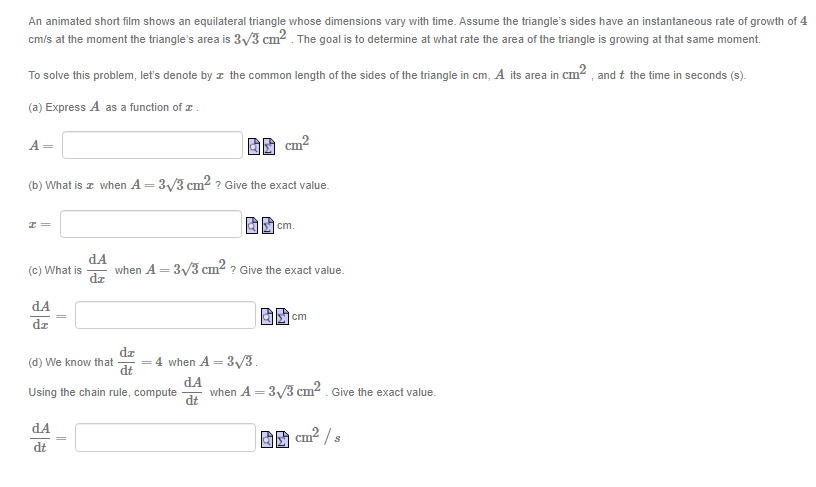
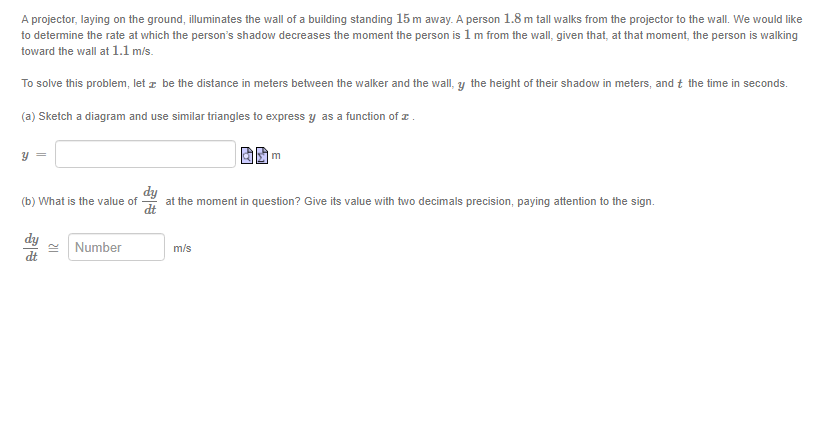
Suppose f is a differentiable function that satisfies 2x f(x) + cos(f(x) - 1) =9 for all r. If f(4) = 1, what is f'(4) ? Answer: f (4) = (You do not need to (nor can you!) find a formula for f(@). Hint: differentiate both sides of the equation with respect to I.)The function y is given implicitly by the equation y' In(y) - x In(r) = 6 Find the derivative of y as a function of r and y Answer: y' =A spherical snowball is melting in the sun. It is noted that its surface area decreases at a rate of 2 cm /s at the moment when its diameter is cm. The goal here is to determine the rate at which the diameter varies at that same moment. To solve this problem, let : be the diameter of the snowball in cm, A its surface area in cm , and t the time in seconds (s). (a) Express A as a function of c . (The surface area is a formula you can find in your textbook.) A = 60 cm2 dA (b) What is the value of when I = ? Give the exact value. dA cm 5 (c) Using our previous results, give the (exact) value of dt when I cm. Beware of signs, remember that the surface area of the snowball is decreasing with time! dt i cm/s.A kite glides horizontally at an altitude of 30 m while we unspool the string. Consequently, the angle made between the string and the horizon diminishes. We would like to determine the rate at which this angle decreases once 40 m of string has been unspooled, given that, at that instant, the kite's horizontal velocity is 1 m/s. To solve this problem, let & be the angle in radians made between the string and the horizontal, r the kite's horizontal position in meters since being attached to the ground, and t the time in seconds. We further suppose that the string is straight and taut. (a) Sketch a diagram of this question and use it to express o as a function of I . BO rad (b) What is the value of c at the moment in question? Give the exact value. de (c) What is the value of dt at the same moment? Give the exact value, paying attention to the sign. de als radisAn animated short lm shows an equilateral triangle whose dimensions var}.I with time.Assume the triangles sides have an instantaneous rate of growth of 4 2 on'u's at the moment the triangle's area is 3']? cm . The goal is to determine at what rate the area ot the triangle is growing at that same moment. 2 To solve this problem. let's denote by :I: the common length ofthe sides of the Inangle in cm, A its area in cm . and t the time in seconds (s). {a} Express A as a function of :I: . A= Ia cm2 {to} W't'lat is :I: when A = 3J3'L'm2 ? Give the exact value. I: .al'l'l. lid (12] What is d when A = 3J3 I::I:I12 ? Give the exact value. 3 (1A E = new do: (cl) We know that E = 4 when A = B. _ _ dd 2 _ Using the chain rule, compute E when A. = 3JEII1 . Give the exact value. (Li H: Ignaz/{s A projector. laying on the ground, illuminates the wall of a building standing 15m away. A person 1.3 rn tall walks from the projector to the wall. We would like to detem'line the rate at which the person's shadow decreases the moment the person is 1 m from the wall. given that. at that moment. the person is walking toward the wall at 1.1 mls. To solve this problem: let 2 be the distance in meters between the walker and the wall. 3; the height of their shadow in meters: and t the time in seconds. (a) Sketch a diagram and use similar triangles to express 3; as a function of I. y = a m (b) What is the value of al the moment in question? Give its Iiralue with two decimals precision: paying attention to the sign. cit II? is; 3 Number ml's