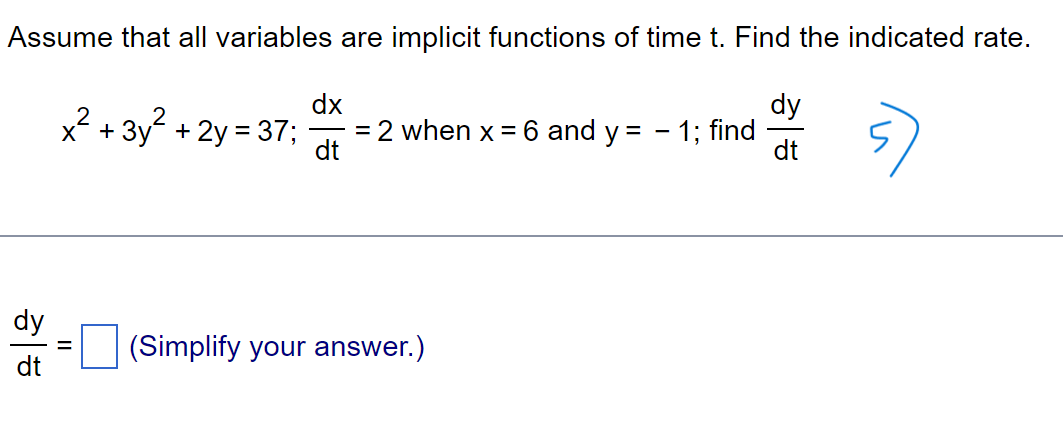
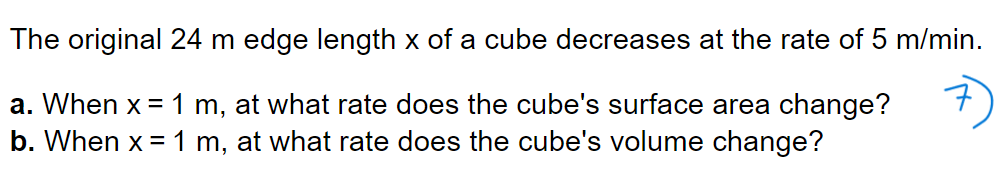
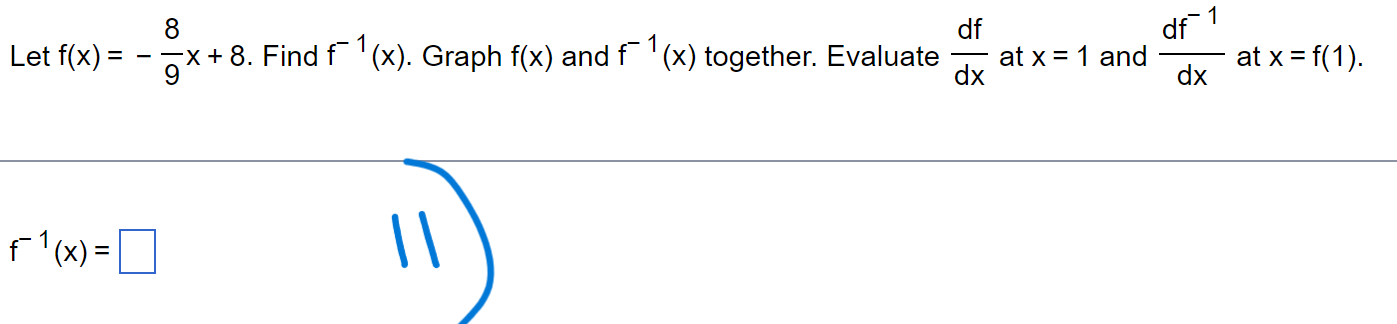
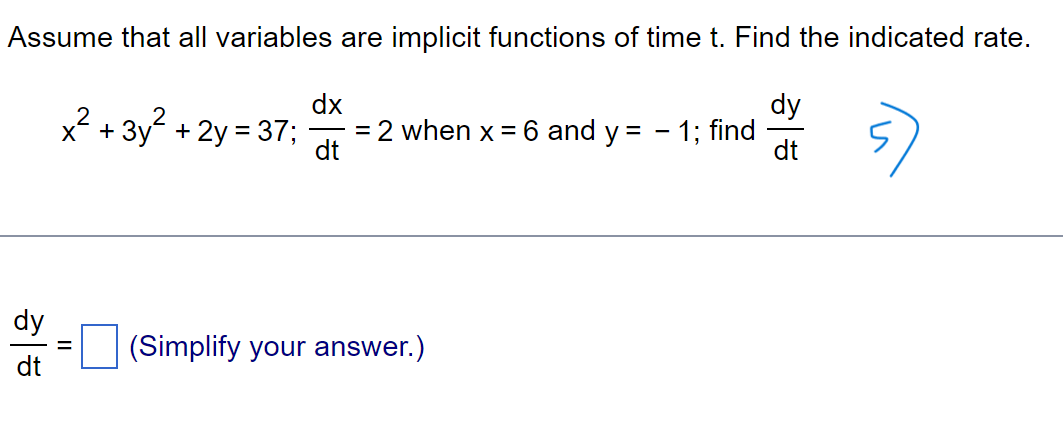
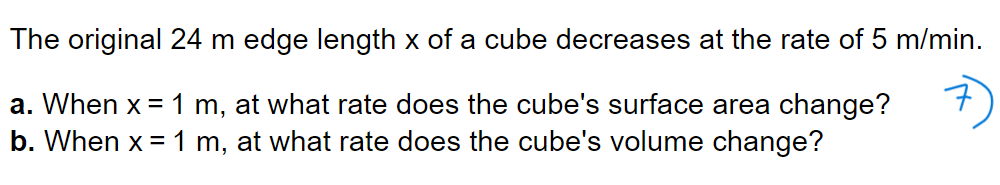
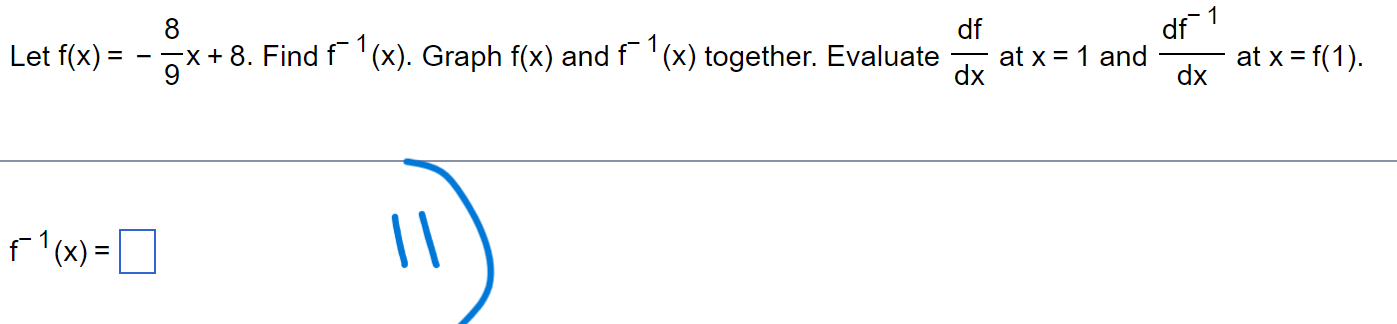
Suppose that a dimension x and the area A = 7x of a shape are differentiable functions of t. Write an equation that relates dA dx to dt dt . . . dA dx dt dtThe dimensions x and y of an object are related to its volume V by the formula V = 9x y. dV dy a. How is related to if x is constant? dt dt 2) dV dx b. How is related to dt if y is constant? dt dV dx dy c. How is dt related to and if neither x nor y is constant? dt dtdx dy Assume that y = 9x and = 8. Find dt dt W dy dt (Simplify your answer.)dx Assume that x = x(t) and y = y(t). Let y = x*+ 3 and =2 when x = 5. dt dy Find when x = 5. dt 4 dy = dt (Simplify your answer. )Assume that all variables are implicit functions of time t. Find the indicated rate. dx dy x2 + 3y 2 + 2y = 37; = 2 when x = 6 and y = - 1; find dt dt dy (Simplify your answer.) dtLet x and y be differentiable functions of t, and let s = 16x-+ 3y be a function of x and y. Answer the following questions. . . . ds dx a. How is dt related to dt if y is constant? ds dx dt dtThe original 24 m edge length x of a cube decreases at the rate of 5 m/min. a. When x = 1 m, at what rate does the cube's surface area change? 73 b. When x = 1 m, at what rate does the cube's volume change? When a circular plate of metal is heated in an oven, its radius increases at a rate of 0.02 cm/min. At what rate is the plate's area increasing when the radius is 52 cm? Write he equation that relates the rate of change in area to the rate of change in radius. \\g dA dr E = a (Type an expression using r as the variable.) When a circular plate of metal is heated in an oven, its radius increases at a rate of 0.04 cm/min. At what rate is the plate's area increasing when the radius is 55 cm? a The rate of change of the area is cmzlmin. (Type an exact answer in terms 0 TC.) Suppose that a drop of mist is a perfect sphere and that. through condensation. the drop picks up moisture at a rate proportional to its surface area. Show that under these circumstances the drop's radius increases at a constant rate. A sphere with radius r has volume V = D and surface area S = D. \\\" df- 1 Let f(x) = 3x - 5x - 4, x2 1.5. Find the value of dx at the point x = 464 = f(6). 13 df 1 The value of dx at the point x = 464 = f(6) is (Type a simplified fraction.)