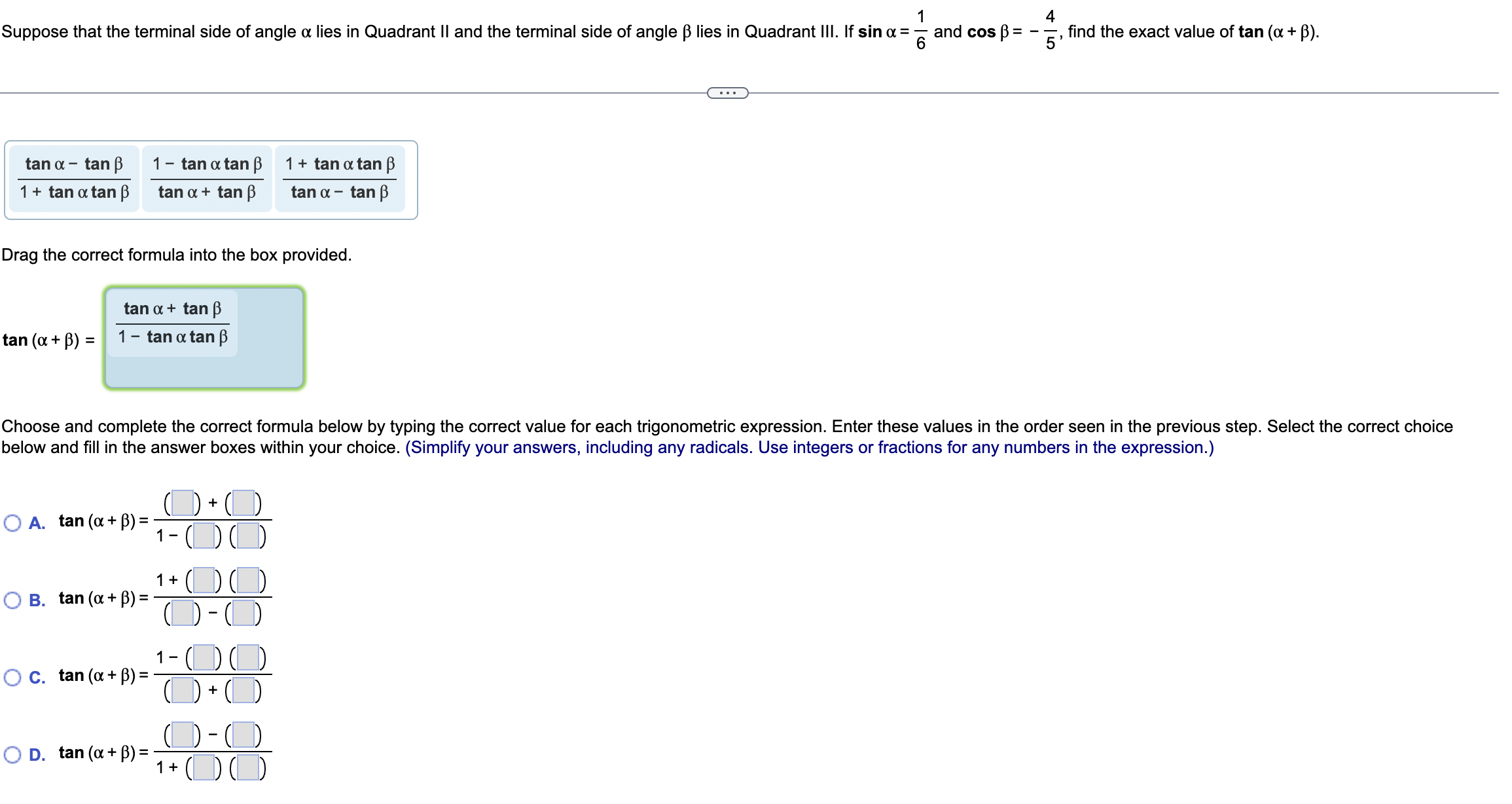
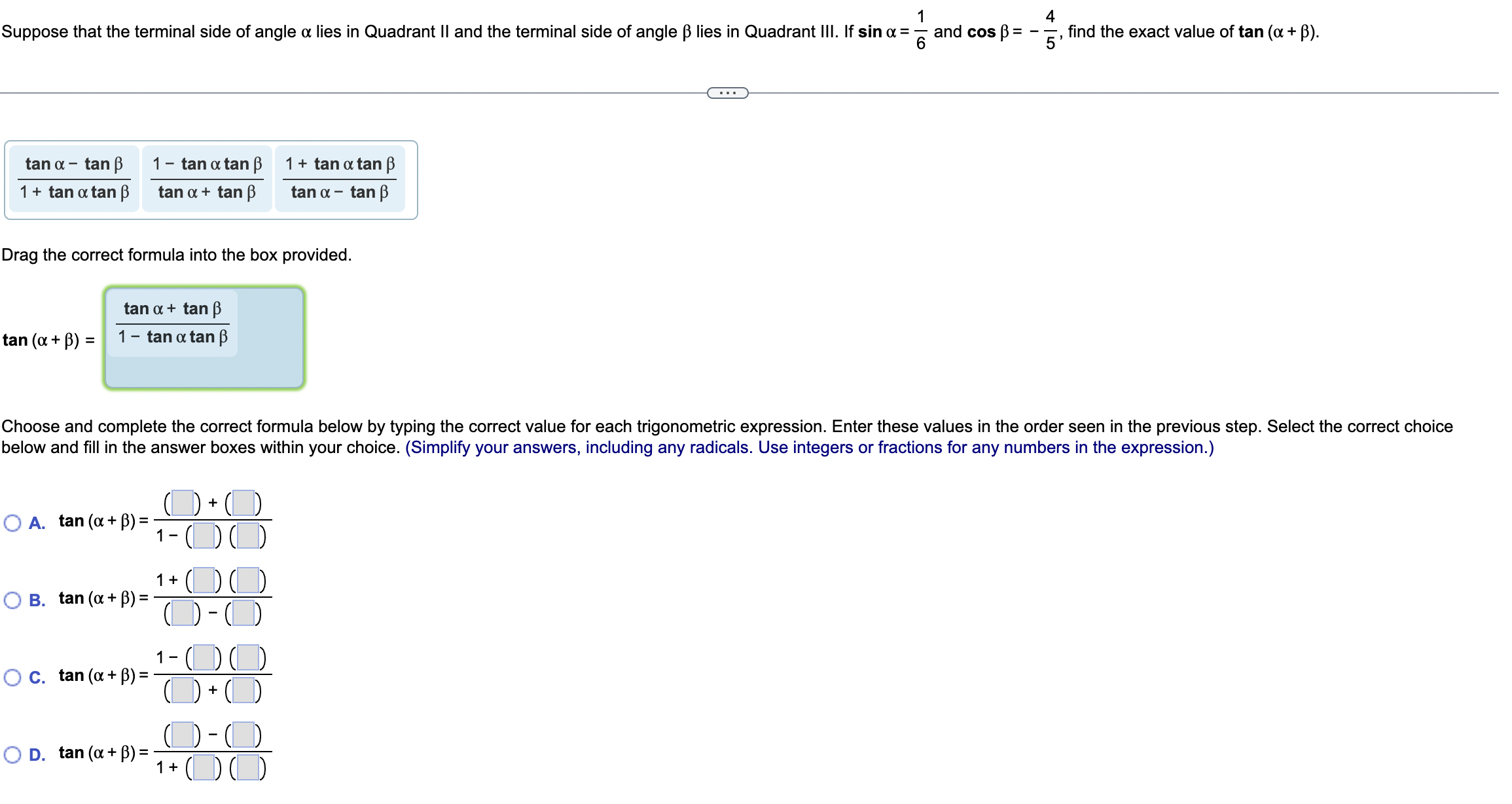
Suppose that a is an angle such that tan a = - and sin 0. Find the exact value of sin (a - B). Choose the correct formula for the sine of the difference of two angles. sin (a - ) = sin a cos B - cos a sin B Choose and complete the correct formula below by typing the correct value for each trigonometric expression. Enter these values in the order seen in the previous step. Select the correct choice below and fill in the answer boxes within your choice. (Simplify your answers, including any radicals. Use integers or fractions for any numbers in the expression.) O A. sin (a - B) = ( ) ( ) - ()() O B. sin (a - B) = ( ) ( ) + ( ) ()4 Suppose that the terminal side of angle a lies in Quadrant II and the terminal side of angle p lies in Quadrant III. If sin a = - and cos B = - -, find the exact value of tan (a + B). 1 tan a - tan B 1 - tan a tan p 1 + tan a tan B 1 + tan a tan B tan a + tan B tan a - tan p Drag the correct formula into the box provided. tan a + tan B tan (a + p) = 1 - tan a tan p Choose and complete the correct formula below by typing the correct value for each trigonometric expression. Enter these values in the order seen in the previous step. Select the correct choice below and fill in the answer boxes within your choice. (Simplify your answers, including any radicals. Use integers or fractions for any numbers in the expression.) ( ) + ( ) O A. tan (a + () = 1 - ( ) ( ) 1 + ( ) ( ) O B. tan (a + B) = ( ) - 0) 1 - ( ) O c. tan (a + B) = ()-0) O D. tan (a + p) = 1 + ( ) ( )