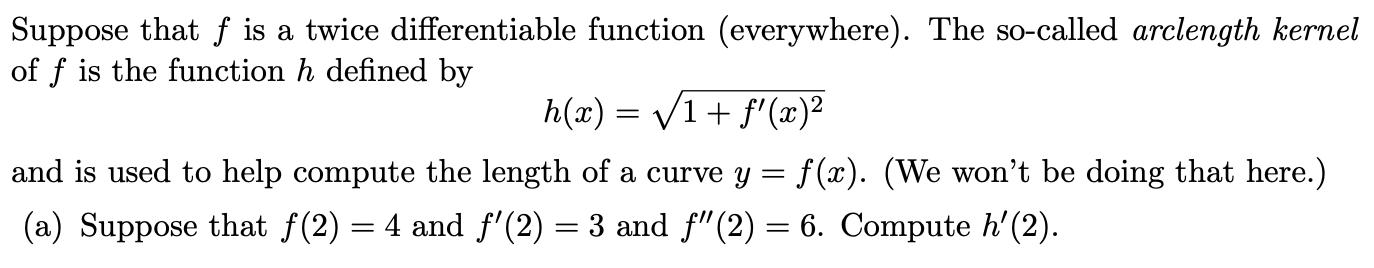
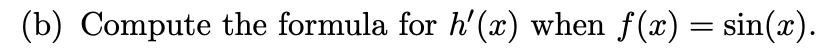
Suppose that f is a twice differentiable function (everywhere). The so-called arclength kernel of f is the function h defined by h(ac) = V1+ f' (x)2 and is used to help compute the length of a curve y = f(x). (We won't be doing that here.) (a) Suppose that f(2) = 4 and f'(2) = 3 and f"(2) = 6. Compute h'(2).(b) Compute the formula for h'(xx) when f(x) = sin(x)