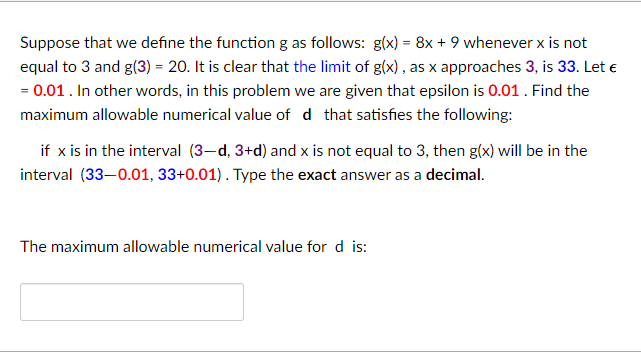
Suppose that we define the function g as follows: g(x) = 8x + 9 whenever x is not equal to 3 and g(3) = 20. It is clear that the limit of g(x) , as x approaches 3, is 33. Let e = 0.01 . In other words, in this problem we are given that epsilon is 0.01 . Find the maximum allowable numerical value of d that satisfies the following: if x is in the interval (3-d, 3+d) and x is not equal to 3, then g(x) will be in the interval (33-0.01, 33+0.01) . Type the exact answer as a decimal. The maximum allowable numerical value for d is