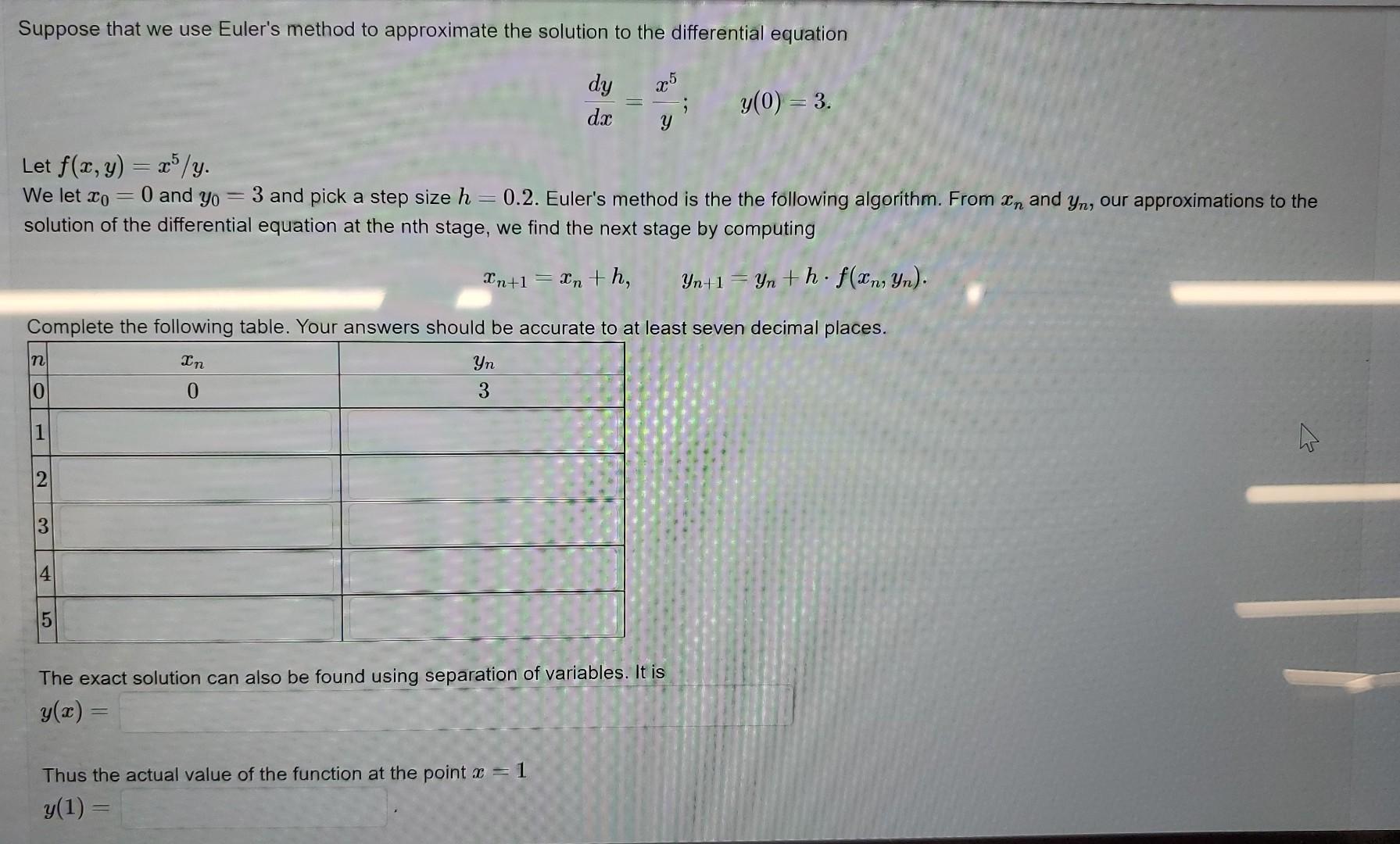
Suppose that we use Euler's method to approximate the solution to the differential equation dxdy=yx5;y(0)=3 Let f(x,y)=x5/y We let x0=0 and y0=3 and pick a step size h=0.2. Euler's method is the the following algorithm. From xn and yn, our approximations to the solution of the differential equation at the nth stage, we find the next stage by computing xn+1=xn+h,yn+1=yn+hf(xn,yn). Complete the following table. Your answers should be accurate to at least seven decimal places. The exact solution can also be found using separation of variables. It is y(x) Thus the actual value of the function at the point x=1 y(1)=