Suppose there are n tasks where each task is associated with an execution time ti and a deadline di. (Consider, for example, the assignments from your various classes and their due dates.) The goal is to schedule the tasks, no two overlapping in time, such that they are all completed before their deadline. If this is not possible, we define the lateness of the ith task to be the amount by which its finish time exceeds its deadline. If job i finishes at time fi, the lateness is defined as li=max{0, fidi}. The goal is to design an algorithm that minimizes the maximum lateness value overall tasks. Here is an example to understand the problem better:

Consider the following two ideas for scheduling the jobs:

(a) Schedule the jobs in the order of smallest duration first

(b) Schedule the jobs in the order of earliest deadline first

Discuss each of these two ideas and decide which one is the best to choose as our greedy approach. In other words, which one will guarantee an optimal solution.

Remember: in order to show an approach fails to give the optimal solution you can give a counterexample. In order to show an approach provides an optimal solution you need to prove it.

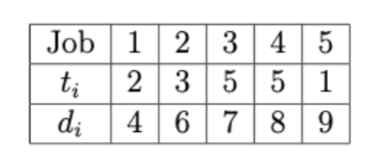
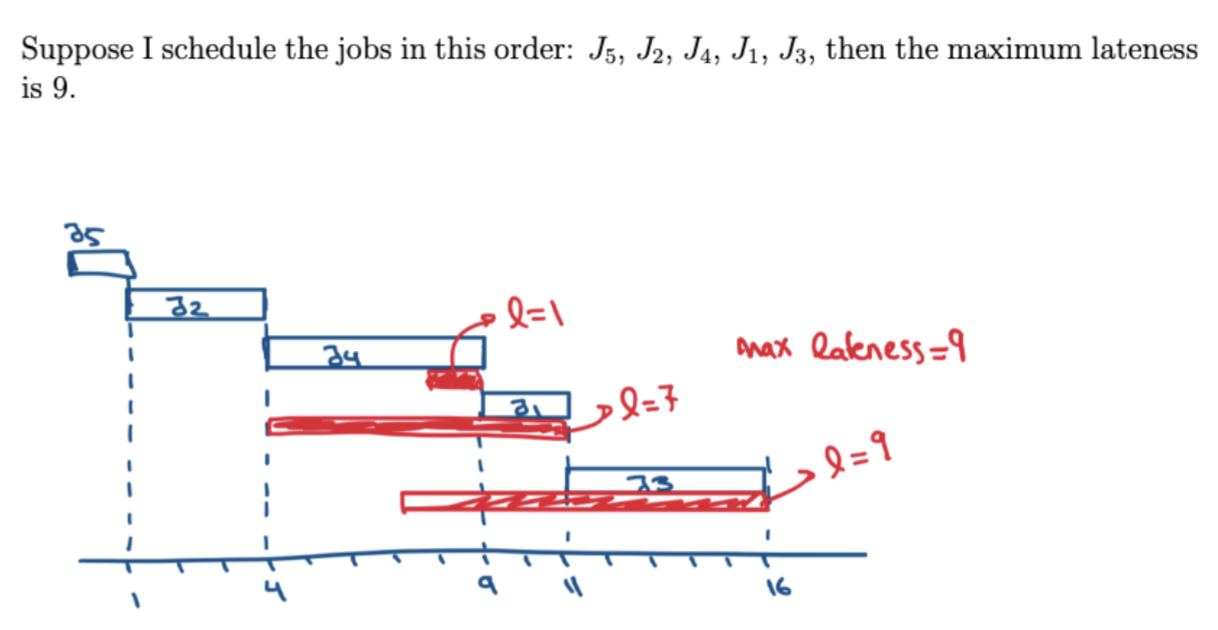
Job 1 2 3 4 45 ti 2 3 5 5 5 1 di 4 6 7 8 9 Suppose I schedule the jobs in this order: J5, J2, J4, J1, J3, then the maximum lateness is 9. J2 b=1 24 max lakness=9 l=7 23 -l=9