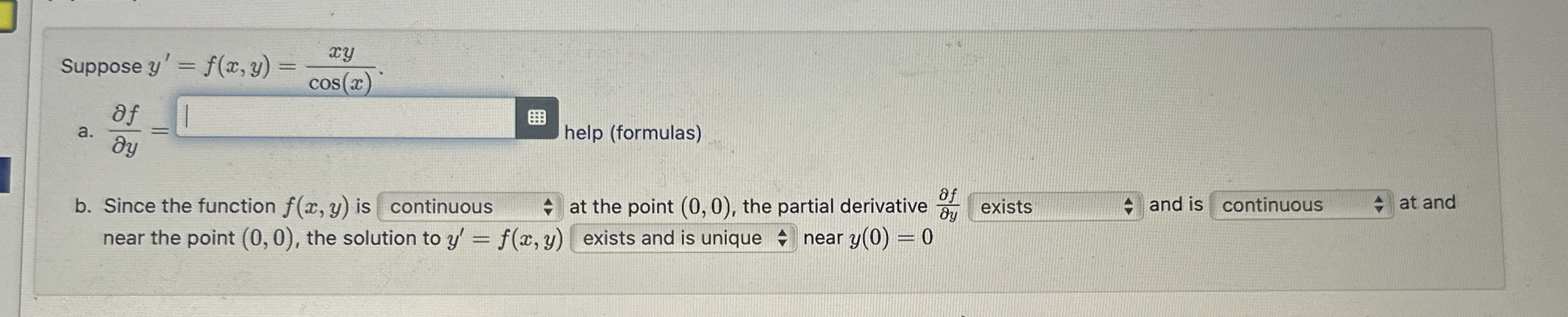
Question: Suppose y ' = f ( x , y ) = x y c o s ( x ) . a . d e l
Suppose
a help formulas
b Since the function is continuous at the point the partial derivative and is at and near the point the solution to exists and is unique near
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


