SYSTEM PROGRAMMING AND OPERATING SYSTEM CODING PROBLEM

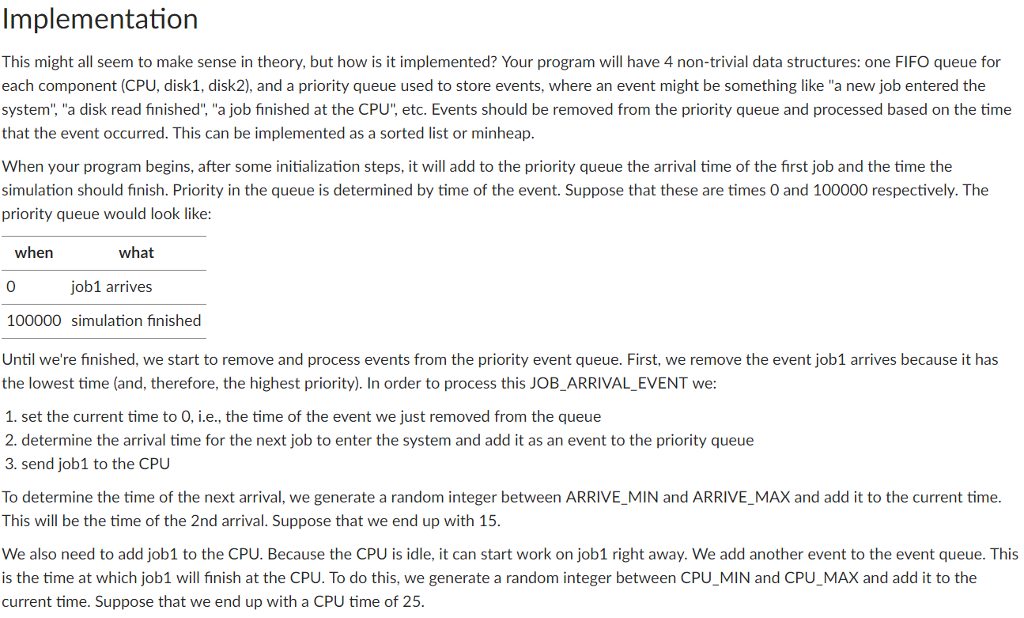
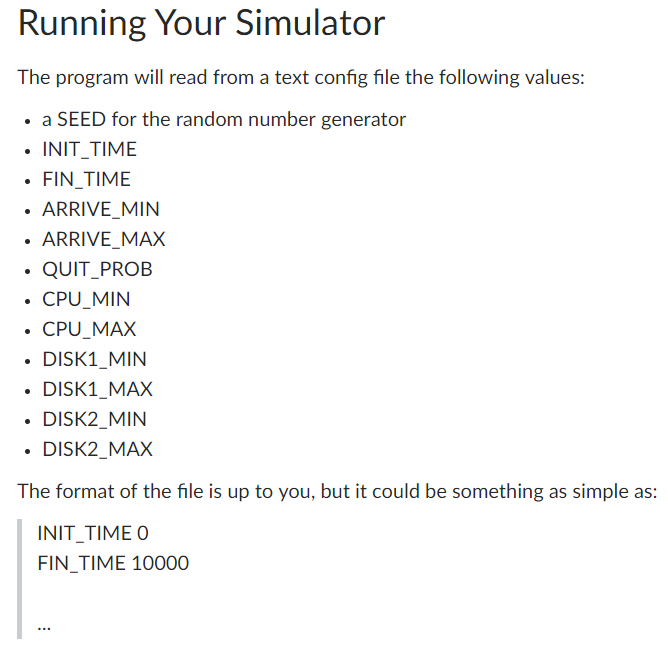
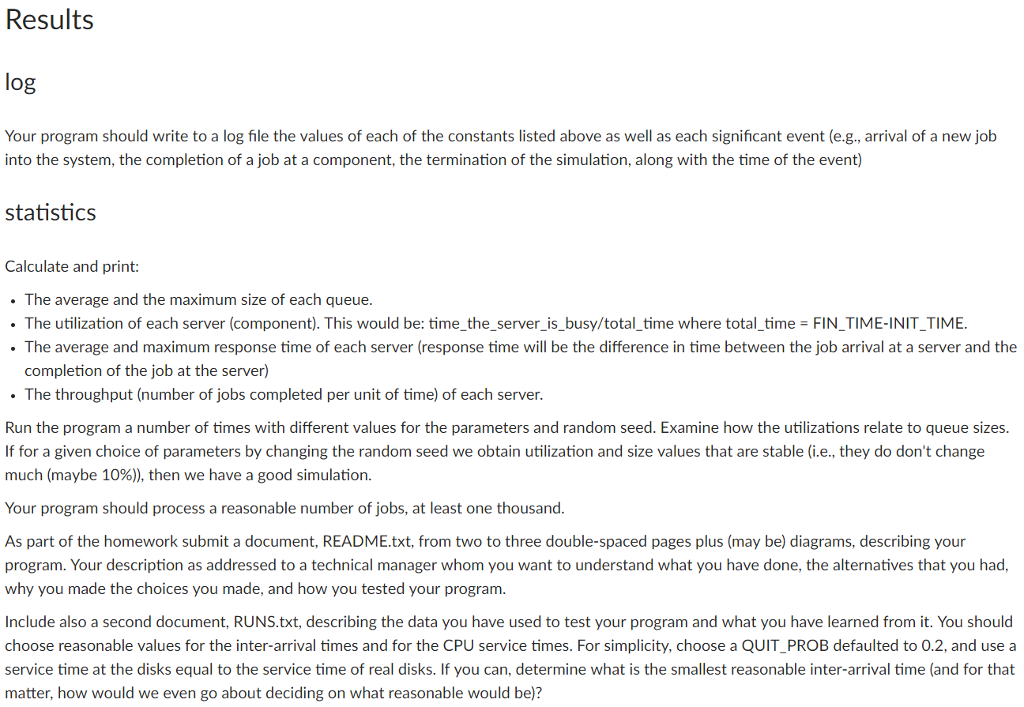
Read requirements carefully and only full answers will get upvoted. Thanks.

Basic Mechanism The system behaves as follows . The system runs from INIT TIME (usually O) to FIN_TIME. . Jobs enter the system with an interarrival time that is uniformly distributed between ARRIVEMIN and ARRIVE_MAX. . Once a job has finished a round of processing at the CPU, the probability that it exits the system (instead of doing a disk read and then further . When a job needs to do disk I/O, it uses the disk that's the least busy, i.e., the disk whose queue is the shortest. (This might seem a bit silly, but . When jobs reach some component (CPU, disk1, or disk2), if that component is free, the job begins service there immediately. If, on the other . The queue for each system component is FIFO computation) is QUIT PROB we can pretend that each disk has the same information.) If the disk queues are of equal length, choose one of the disks at random hand, that component is busy servicing someone else, the job must wait in that component's queue. . When a job reaches a component (a different job leaves a component or the component is free, and this job is first in the queue), how much time does it spend using the component? This is determined randomly, at runtime, for every component arrival. A job is serviced by a component for an interval of time that is uniformly distributed between some minimum and maximum defined for that component. For example, you'll define CPU_MIN, CPU_MAX, DISK1 MIN, DISK1_MAX, etc. . At time FIN_TIME, the job simulation terminates. We can ignore the jobs that might be left receiving service or waiting in queue. Basic Mechanism The system behaves as follows . The system runs from INIT TIME (usually O) to FIN_TIME. . Jobs enter the system with an interarrival time that is uniformly distributed between ARRIVEMIN and ARRIVE_MAX. . Once a job has finished a round of processing at the CPU, the probability that it exits the system (instead of doing a disk read and then further . When a job needs to do disk I/O, it uses the disk that's the least busy, i.e., the disk whose queue is the shortest. (This might seem a bit silly, but . When jobs reach some component (CPU, disk1, or disk2), if that component is free, the job begins service there immediately. If, on the other . The queue for each system component is FIFO computation) is QUIT PROB we can pretend that each disk has the same information.) If the disk queues are of equal length, choose one of the disks at random hand, that component is busy servicing someone else, the job must wait in that component's queue. . When a job reaches a component (a different job leaves a component or the component is free, and this job is first in the queue), how much time does it spend using the component? This is determined randomly, at runtime, for every component arrival. A job is serviced by a component for an interval of time that is uniformly distributed between some minimum and maximum defined for that component. For example, you'll define CPU_MIN, CPU_MAX, DISK1 MIN, DISK1_MAX, etc. . At time FIN_TIME, the job simulation terminates. We can ignore the jobs that might be left receiving service or waiting in queue