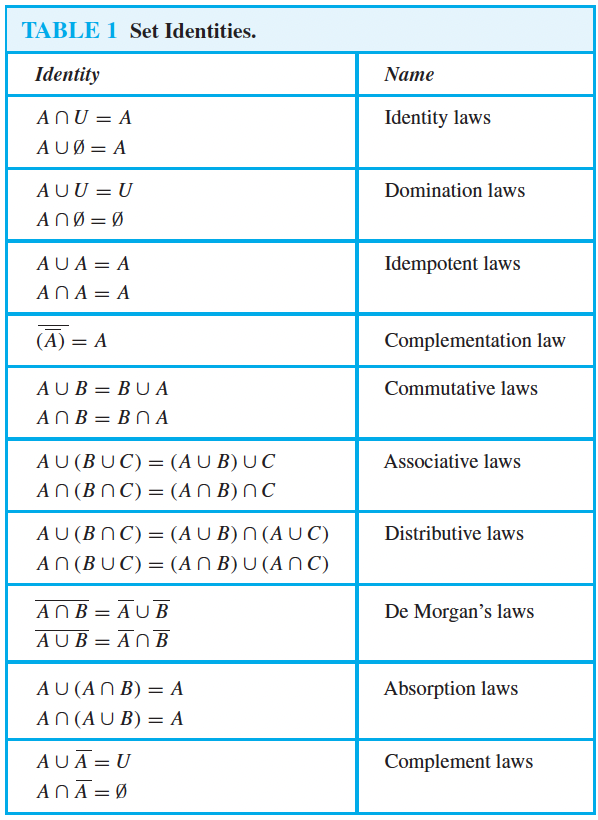
TABLE 1 Set Identities. Identity Name AnU = A Identity laws AUD = A A UU = U Domination laws And =0 AUA = A Idempotent laws AnA = A (A) = A Complementation law AUB = BUA Commutative laws AnB = BOA AU(BUC) = (AUB) UC Associative laws An(BAC) = (AnB)nc AU(BOC) = (AUB) n(A UC) Distributive laws An(BUC) = (AnB) U (AnC) AnB = AUB De Morgan's laws AUB = AnB AU(AnB) = A Absorption laws An(AUB) = A A UA = U Complement laws AnA =0MTH 309 Additional Problems for Sec 2.2 1. Prove one of the distributive laws of sets in Table 1 by using set builder notation and the corresponding law of logic. 2. Prove one of the absorption laws of sets in Table 1 by using set builder notation and the corresponding law of logic 3. Use the set identities in Table 1 to prove the following identities (be sure to give the identity being used at each step): (a) (AUB)UA=A (b) AN(B-C)=(ANnB)(ANC)